Introduction
Over 20 years ago, shortly after the standardisation of SGML in 1986 (Gold90), the problem of overlap was first noticed as a serious difficulty in the encoding of digital texts in the humanities and linguistics (Barn88). Overlap may be defined as the inability of markup systems to easily represent overlapping structures by means of paired tags whose primary function is to contain text or other markup in a strictly nested and ‘well-formed’ way (Bray08, 2.1). Barnard et al. (Barn88, 275) reassured the reader at the time that ‘SGML can successfully cope with the problem of maintaining multiple structural views’ and that the ‘solutions can be made practical’. After around 50 papers and theses later it would seem that this early assessment may have underestimated the extent of the problem. There have been many surveys of the literature on the subject (Witt02; Maas03; Dero04), but the consensus seems to be that no general solution to the overlap problem is known or likely (Maas03, 18; Sahl05, 3).
The Multi-Version Document or MVD format has been put forward as a possible general solution to the overlap problem (Schm09). Although originally conceived as a solution to textual variation, an MVD can also be used to represent ‘overlapping hierarchies’, since multiple conflicting markup perspectives of a single linear text can be construed as variant texts in which only the markup varies. An MVD represents both overlap and variation by replacing the conventional linear form of text with a directed graph. This graph may take two forms:
-
As an explicit directed acyclic graph that starts at one point, then diverges and remerges as required, before ending again at a single point. I call this a ‘variant graph’. Each arc is labelled with the set of versions to which that arc belongs, and a fragment of text, which may be empty. Any version can be read by following the appropriate path through the graph from start to finish. Figure 1 shows a variant graph generated using the algorithm described in this paper from three versions (labelled A,B,C) of part of Valerio Magrelli’s Italian poem Campagna romana (Magr81).
-
As a list of interleaved pairs, consisting of the labels of each arc, and the sets of versions to which it belongs. The pairs are ordered so that the labels preserve the order of the text for each version they represent (Figure 2).

Figure 1: A Variant Graph

Figure 2: Part of the Same Graph as a List of Pairs
These two forms are equivalent and interchangeable. The list form is currently better for searching, listing, saving and comparing two versions in an MVD, and the explicit graph for creating and editing an MVD. Conversion between the two forms can be performed losslessly in essentially linear time. It is hoped that in the future it will also be possible to edit and create MVDs using the simpler list format.
Advantages of the MVD Format
-
Because an MVD doesn’t know anything about the format of the text contained in each arc-label or pair, any technology can be used to represent the content of an individual version. In this way the complex overlapping structures of the text are abstracted out into the graph structure, so that the content can be represented using conventional, and simplified, markup. This allows the reuse of existing markup-based tools such as XSLT (Figure 3).
-
Representing a work that contains multiple versions or markup perspectives as a single digital entity facilitates searching, comparing, editing and transmission of the work without the need for complex software to integrate a set of separate files.
-
Because the MVD representation is very simple, and is not dependent on markup, it can provide a general solution to the overlap problem in corpus linguistics and humanities texts of various types and dates. It can work equally well with plain text and some binary formats.
The only real disadvantage of the format is the difficulty of producing it automatically, which is the problem this paper attempts to solve.

Figure 3: Separation of Variation from Content
Operations on MVDs
The commonest operations that may be performed on MVDs include:
-
Listing a given version
-
Comparing two versions
-
Searching a multi-version text
-
Finding out what is a variant of what
-
Creating and updating an MVD
An MVD may be created by successively adding versions to an initially empty document. Updating an existing version can be performed in the same way by first deleting the version to be replaced. Creating and updating an MVD thus both reduce to the same operation: that of merging a single version into an existing multi-version document.
Analogies to the Current Problem
The basic problem that underlies this merging operation has already been researched in other fields, in particular in bioinformatics, text processing and humanities computing. Since the solutions in these areas work with different data and with different objectives, none of these algorithms provide a precise match with the current problem. Nevertheless, examining similar areas of research like this is likely to reveal potential pitfalls as well as furnish possible components of the required solution.
Bioinformatics
Biologists have studied the computational alignment of multiple sequences of nucleic and amino acids for over 40 years. These computations reduce to the finding of insertions, deletions, substitutions and transpositions in texts with a restricted alphabet of 4 characters for nucleotides or 20 for amino acids. There are in fact three main sub-fields within bioinformatics that are relevant to the current problem.
Multiple Sequence Alignment
Biologists frequently search databases for similar sequences to newly sequenced genes or proteins (Lesk02, 177). The results, however, are usually a set of close matches whose interrelationships may need further exploration. For example, it is often of interest to trace the evolutionary history of a series of mutation events that gave rise to different versions of a protein. This is the multiple sequence alignment problem (Edga06).
Two-Way Global Alignment
A multiple sequence alignment is usually built up from a series of two-way alignments, for which an optimal dynamic programming solution has existed since 1970 (Need70). This calculates a ‘global’ alignment, because it aligns every character in the two sequences.

Figure 4: Needleman-Wunsch Algorithm
In Figure 4 a 2-D matrix representing the alignment of the two strings is filled from the bottom right-hand corner to the top left-hand corner, one cell at a time. Each cell is filled with 1 if the letters at those coordinates match, otherwise 0, plus the maximum cell-value of the next row and column down and to the right. Once filled, the matrix can be used to recover a common subsequence with the highest score by following matching pairs from 0,0 down and to the right. There may be more than one such optimal path through the matrix.
Although it is theoretically possible to extend their method to n sequences, the time and space requirements increase exponentially for n > 2. For this reason only the 2-way alignments of all possible pairs of sequences are normally computed, which are then used to construct a close approximation to a global n-way alignment. Even this shortcut turns out to be quite expensive, since the number of possible pairs of n sequences is n(n-1)/2. And the computation of the alignment for each pair of sequences also costs O(MN(M+N)) time, where N and M are the lengths of the two sequences. To give some idea of just how costly that is, the computation of the optimal pairwise alignments of the 36 versions of the Sibylline Gospel (Schm08), i.e. 630 pairwise combinations, each around 2,500 characters long, took 6.6 hours on an ordinary desktop computer.
Progressive Alignment
One popular way of aligning multiple sequences is progressive alignment (Feng87). In this method the global pairwise alignments of a set of sequences are scored for similarity and the results are used to construct a phylogenetic tree, which records the stemmatic relationships between sequences, to act as a ‘guide’ for the merging process. The multiple-sequence alignment or MSA (Figure 5) is then built up by starting with the most similar pair of sequences, adding gaps where needed (and never removed once inserted), then gradually adding in the other sequences as dictated by the guide-tree. Modern examples of this approach include CLUSTALW (Thom94) and T-COFFEE (Notr00), although the latter augments the usual progressive technique with iterative refinement.

Figure 5: Multiple Sequence Alignment
Disadvantages of Progressive Alignment
Because this method was originally developed to handle short sequences, it doesn’t take account of transpositions, or repeated segments, which appear to be common features of longer protein sequences (Pevz04; Delc02; Gu99).
Also, it is a greedy algorithm sensitive to the order in which the sequences are added to the MSA. Alignment errors that occur early on get locked in and lead to greater divergences later (Thom94).
The initial pairwise alignments are particularly expensive to calculate. This limits the number and length of sequences that can be aligned.
Progressive alignment is based on the concept of edit distance (Leve66). This is a count of the number of insertions, deletions and substitutions of individual characters that need to be performed to turn one string into another. This can only ever approximate the real biological processes that gave rise to the differences (Lass02, 13; Lesk02, 168).
Partial Order Alignment
A relatively new technique of multiple sequence alignment called POA or Partial Order Alignment has been described by Lee et al. (Lee02) and Grasso et al. (Gras04). The roots of their method go back to Morgenstern’s Dialign program (Morg96). In that method, as in MAFFT (Kato02), highly similar regions within two sequences are first identified. They are then resolved into a non-overlapping set of diagonals in n Dimensions, then added to the MSA using a greedy strategy. Unaligned regions are then processed recursively. The difference here is that gaps are no longer explicitly introduced: they are simply what is left over once the aligned portions have been determined.
POA takes this strategy one step further: it replaces the MSA matrix with a directed graph. Instead of pairwise alignment they align each successive sequence – in no particular order – to a partly-built PO-MSA (Partial Order Multiple Sequence Alignment). In their method the initial computation of n(n-1)/2 pairwise alignments is not a preliminary step, but is instead integrated into the alignment process. Because a PO-MSA contains far less data than that contained in all possible pairs of sequences, the computational cost is drastically reduced.
Figure 6 shows their adaptation of the dynamic programming method to the directed graph structure. Instead of aligning two linear sequences within a flat 2-D matrix, in the the PO-MSA method the 2-D matrix becomes a complex planar surface corresponding to the partly merged structure of the directed graph, on the one hand, and the new linear sequence, on the other. At each join between surfaces the program has to decide which surface to align with. Regardless of the order in which the sequences are added to the alignment, each possible pairwise combination of sequences will be considered, since each new sequence is compared to all those already in the graph.

Figure 6: PO-MSA Alignment
The speed of the program is impressive, but the quality of the alignments is somewhat less than could be achieved by traditional progressive alignment techniques (Lass02). Grasso et al. (Gras04) think the cause is partly that the original algorithm still appears to be sensitive to the order in which sequences are added to the PO-MSA. This is probably because, unlike the progressive method, each new version is aligned only with those versions already in the graph, not with those still to be added.
Disadvantages of POA
In spite of its innovative data model, the POA graph and associated software can’t handle transpositions or repeated segments. The remaining order sensitivity seems to be an inherent deficiency of this approach.
de Bruijn and A-Bruijn Graphs
The second area in bioinformatics that provides a close analogy to the current problem is a more radical solution to the multiple sequence alignment problem. It evolved from the related field of contig-assembly. Starting in the 1980s DNA sequencing machines were developed which output fragments of DNA, typically 650 base pairs in length (Delc02, 2480). These short segments have to be assembled correctly into longer ‘contigs,’ which is an NP-hard problem. Pevzner (Pevz89), Idury and Waterman (Idur95) and Pevzner (Pevz01) developed a heuristic method in which each DNA fragment was broken up into a series of short overlapping substrings of fixed length. For example, if all possible substrings of length 3 are calculated for the string ‘AGTCGTATAC’, then the original string can be reassembled by overlapping these substrings to form the directed graph of Figure 7.
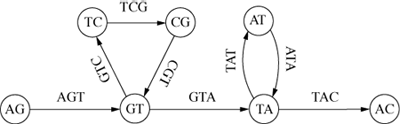
Figure 7: A Sequence Graph
Each node represents two characters shared by its two adjacent arcs, which are labelled with the 3-character substrings. The cycles record the repeats ‘GT’ and ‘TA’. In practice the length of the substrings would be much greater than 3 – around 20 or so (Pevz01, 9751).
This enabled them to reduce the contig-asssembly problem to one of finding an ‘Eulerian’ path through the graph. An Eulerian path is one that visits each arc exactly once, although Idury and Waterman (Idur95, 295) interpret this to mean a path that may cross the same arc multiple times as if it were a set of parallel arcs. The problem can then be solved in linear time by Fleury's algorithm (Aldo00, 202).
The original de Bruijn graph represented all possible strings of length k over an alphabet A and was entirely cyclical (Debr46; Good46). An example is shown in Figure 8, which shows all the 3-character sequences of the alphabet {0,1}.
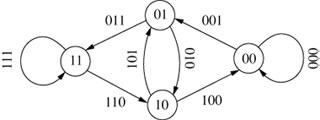
Figure 8: A De Bruijn or Good Graph
Raphael et al.'s approach is to add insertions and deletions to the ‘de Bruijn’ graph, calling the result an A-Bruijn graph, and to use it as their data representation (Raph04). Although they succeed in representing transpositions (or ‘shuffles’) and repeats, their method only aligns the highly similar regions of protein sequences, while the rest is processed separately using progressive alignment techniques.
Disadvantages of de Bruijn and A-Bruijn Graphs
Using directed cycles to represent transpositions leads to complications, as admitted by Pevzner (Pevz01, 9571). For example, if there are several arcs exiting a multiple arc, which of them does one take, and in what order? And what if different sequences need to traverse a multiple arc a different number of times? These complications, although they may be overcome by careful labeling of the arcs, are unnecessary. A variant graph represents transpositions without cycles (Schm09) and repeats can be treated as transpositions in the same version.
Also, what can be the advantage in breaking up the text and multiplying the amount of data by a factor of twenty, then joining it all back up again? Pevzner et al. admit that this actually throws away information, which has to be restored later (Pevz01, 9748).
The A-Bruijn graph also doesn’t appear to be editable.
Discussion
It is interesting that biologists have now recognised that a useful way to represent multiple sequence alignments might be to use a directed graph instead of a matrix, although they have not yet worked out how best to do this. The mere fact that these approaches are an active area of research, and resemble the variant graph approach, provides a vindication of the overall MVD strategy. Many of the same problems described above will also need to be dealt with when formulating a solution to the current problem.
Anchor-Based Aligners
The third area of bioinformatics that overlaps with the current problem has developed only recently. As a result of the successful sequencing of entire genomes, biologists became interested in much larger scale alignments than had been possible via traditional multiple sequence alignment. The limitation is imposed by the dynamic programming technique and its essentially O(N2) performance and space requirements per pair of sequences. Also, at the level of millions of base pairs, relocation, reversal and duplication events have become impossible to ignore.
This need has been met by the rapid development of fragment based aligners, using an anchoring strategy, similar to Heckel's (Heck78) algorithm. Anchoring is the process of first identifying the most similar parts of two or more sequences. Once those have been identified and merged, the program searches for further alignments in the unmerged portions of the sequences. The early fragment based aligners worked only with two versions, e.g. MUMmer (Delc02); MultiPipMaker, based on BLASTZ (Schw00); Avid (Bray03) and LAGAN (Brud03a), and do not handle transpositions, reversals and duplications within the two sequences being compared.
Shuffle-LAGAN
Shuffle-Lagan or SLAGAN (Brud03b) was the first algorithm to add these more advanced editorial operations. However, the authors decline to define a mathematical model for these events and their costs (i56). The program is not symmetric: two different results will be obtained if the two sequences are presented in the opposite order. It is also rather slow; the authors quote a running time of 25 CPU-days to align the human and mouse genomes (i56).
Mauve
Mauve (Darl04) handles transpositions, reversals and duplications, and multiple long sequences. Like the other fragment-based alignment programs, Mauve is based on anchors. The alignment process is shown in Figure 9.
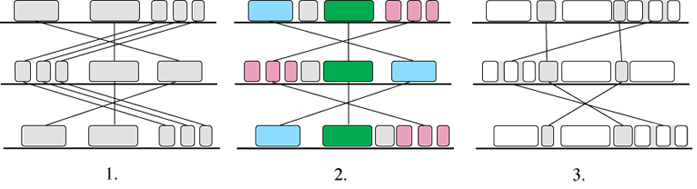
Figure 9: Anchor-based Alignment in Mauve
In the first stage the program searches for Maximal Unique Matches across all the versions, the so-called ‘multiMUMs’. The multiMUMs are used to generate a phylogenetic guide tree. Successive multiMUMs that don’t overlap are then merged into local co-linear blocks or LCBs (2). These act as anchors and allow the identification of further multi-MUMs within and between the LCBs. The identification and merging of LCBs then proceeds recursively (3). Finally, progressive alignment is performed on each LCB using the guide tree.
The authors don’t say how fast it is, but it must be slower than Shuffle-LAGAN since it deals with more versions and uses progressive alignment. Its weakest point appears to be that it has no special data representation for the transpositions, and instead uses colour and interconnecting lines to adapt the traditional MSA matrix display.
Discussion
Unlike the dynamic programming techniques considered earlier, fragment based approaches are able to process much longer sequences. They are also able to identify transpositions. If the progressive alignment stage is removed, they also have the potential to be very fast.
Transposition Algorithms
The transposition operation, which is a key part of the current problem, has been little studied in the fields of source code management (version control) and text processing. For these purposes simply calculating the insertions and deletions between two texts at a time, the so-called ‘diffs’ usually suffices. Tichy (Tich84), for example, reports that adding transposition to the standard diff algorithm for source code management systems only improved performance by 7%. Apart from a couple of practical algorithms for computing transpositions, most of the work is theoretical.
Heckel's 1978 algorithm is the earliest known (Heck78). It first identifies all the unique lines shared by the two strings, and extends them on either side as long as they match in both versions. If the order of these blocks differs in the two versions they are considered transposed, and otherwise aligned. His method, however, fails if there are no unique lines shared by the two strings.
Tichy (Tich84) proposed a linear time algorithm using a suffix tree for finding what he called the ‘minimal covering set’ of block moves between two strings. He defines a covering set to mean that every character appearing in both strings is covered by some block move. As shown in Figure 10, a minimal set is just a set of such moves of minimal size. Neither string need be entirely covered by the moves, however, and the moves may overlap.
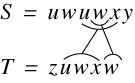
Figure 10: Tichy's Minimal Covering Set
On the theoretical side, the complexity of the transposition problem was first investigated by Wagner (Wagn75). He proved that even the addition of simple transpositions of two adjacent characters changes the computational complexity of the edit distance problem from quadratic to NP-complete.
The edit distance problem with block moves was then investigated in depth by Lopresti and Tomkins (Lopr97). They examined variations of the problem in which:
-
The blocks are disjoint, i.e. they don’t overlap, denoted by D, or if they do by
 .
.
-
The blocks form a cover, i.e. the transposed blocks occupy all of the text, denoted by C or by
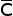 if they don’t.
if they don’t.
For each of the possible combinations of C,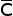 ,D,
,D, they examined the cost of computing the string edit distance between two strings
A and B. Using the C,D notation the CD-CD problem is the computation of the string
edit distance for a disjoint cover for strings A and B. They reduce each such combination
to job scheduling – a known NP-complete problem (Gare79). They conclude that the only variations that are not NP-complete are those involving
they examined the cost of computing the string edit distance between two strings
A and B. Using the C,D notation the CD-CD problem is the computation of the string
edit distance for a disjoint cover for strings A and B. They reduce each such combination
to job scheduling – a known NP-complete problem (Gare79). They conclude that the only variations that are not NP-complete are those involving
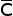
 for one of the sequences. It is clear that the current problem here is
for one of the sequences. It is clear that the current problem here is 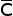 D-
D- D, which is NP-complete. These results are confirmed by Shapira and Storer (Shap02).
D, which is NP-complete. These results are confirmed by Shapira and Storer (Shap02).
Discussion
The practical solutions in this section are not much use for the current problem since they only deal with two versions at a time. Also, since the current problem is NP-complete, it will not be possible to design an algorithm to calculate an optimal solution with respect to edit distance. This is not as bad a result as it seems, since:
-
there is no generally agreed measure of edit distance for transpositions, as there is for insertions, deletions and substitutions
-
just as evolutionary events are not precisely modelled by edit distance, so too an ‘optimal’ alignment in a computational sense may not correspond to an optimal alignment in an aesthetic sense.
A well-designed heuristic algorithm, then, might actually produce better results, as well as take less time.
Collation Algorithms
The third area of analogous research belongs to the more familiar field of humanities computing. A collation program is designed to automate a manual task: the comparison of a number of texts to discover their differences, and output them as an apparatus criticus (Shil96, 134). These differences could then be used to construct a stemma or phylogenetic tree, which would in turn be used in the establishment of the one ‘true’ text (Gree94, 359-360). Clearly, this process belongs to the age of print, but even in the modern digital era there is still a need to compare texts. The current problem can be regarded as a reframing of that process for the digital medium.
Sliding Window Collators
Froger (Frog68, 230) describes the execution of what was probably the world's first collation program, running on a Bull GE-55 computer that had only 5K of internal memory. It compared two texts, one word at a time. If there was a mismatch the program gradually increased its lookahead to 2, 5, 25, ... words, comparing all of the words with one another in this window until it found a match, then sliding the window on by one word at a time. This allowed it to recognise insertions, deletions and substitutions over short distances.
This sliding window design, although later much enhanced, appears to have been the basis of all collating programs until recently. Its main disadvantages are that it can’t recognise transpositions, and that it will fail to correctly align inserted or deleted sections larger than its window size. Computational complexity for each pair of versions is O(NW2), where W is the sliding window size, and N is the average length of the two sequences. Typically a modern collation program will compare each version against a single, and possibly idealistic, base text. Examples include COLLATE (Robi89, 102) and TUSTEP (Ott00).
Progressive Alignment
Spencer and Howe (Spen04) apply biological progressive alignment to medieval texts of the Canterbury Tales and Parzival. They point out that current automatic collation techniques mimic the original manual process too closely. In particular they object that comparing each version against a base text omits important comparisons between individual witnesses. However, their main objective is to generate a phylogenetic tree or stemma, rather than to produce an apparatus.
JUXTA
JUXTA (Mcga06) is an open source program, whose collation algorithm is an adaptation of Heckel's (1978). The adaptation consists in reducing the granularity from a line to a word, and in calling it recursively on the unaligned parts. JUXTA collates plain text with embedded empty XML elements as milestone references, like the COCOA references in COLLATE. JUXTA can also be used to produce an apparatus criticus.
MEDITE
MEDITE (Bour07) is a two-way alignment algorithm based loosely on the fragment based aligners Shuffle-LAGAN and Mauve. The advantage of this approach, in which the transpositions and matches are identified first, then substitutions, insertions and deletions, is that a linear performance can be achieved. The algorithm is basically:
-
Normalise the two texts in some predefined way, e.g. removal of punctuation, reduction to lowercase, removal of accents etc.
-
Build a generalised suffix tree between strings A and B, as described in (Gusf97, 125). This calculates MUMs between the two strings in linear time.
-
Decide which matches are aligned and which are transposed. Since the number of combinations of matches generated by step 2 is exponential, a LIS heuristic (Guye97) is used to find a good alignment.
-
Repeat steps 2 and 3 recursively between each pair of aligned blocks.
Disadvantages of Collation
Collation algorithms have several potential weaknesses. They are mostly slow, and generally collate plain text, rather than XML. Nowadays transcriptions of documents in linguistics and the humanities are more likely to be in some form of XML. The problem is that if one collates XML, then the generated apparatus will contain unmatched tags. Markup will then have to be ignored, but that means losing valuable information.
The inclusion of COCOA or empty XML references embedded in the text precludes the use of any other kind of markup, such as structural markup. But references are only needed for attaching the apparatus to the main text, and this could be done away with in a purely digital edition.
Comparison needs to be between all versions at once. Currently only Spencer and Howe's (Spen04) method achieves this.
Transpositions need to be detected, especially when a work is witnessed by many independent copies. Few of the algorithms do this, and none over n versions.
Taken together, the most advanced algorithm appears to be Bourdaillet's (Bour07). However, it can only consider two versions at a time, and so cannot be directly applied to the current problem.
A Fast Algorithm to Merge n Versions with Block Moves
The preceding sections have described the various techniques and pitfalls of aligning n versions with or without block transpositions. As explained at the beginning of this paper, if the MVD concept is to become a viable solution, some means must be provided to update an MVD with the text of a new or existing version. This can only be achieved if a number of conditions are met:
-
It has to work in ‘real’ time, so that the user doesn’t lose interest in the process. In other words, the algorithm must terminate correctly in the order of seconds, rather than minutes, hours or days.
-
It has to detect transpositions automatically.
-
It doesn’t have to produce 100% accurate alignments, but it should be accurate enough for the user not to notice.
-
It needs to update by aligning the new version with all versions currently in the MVD. Otherwise editing will gradually degrade the quality of the alignment.
Alignment Without Transposing
Before considering the complications arising from transpositions, the algorithm’s processing of direct alignments will be described. This will simplify the transposition case and provide a better overall understanding of how the algorithm works. For direct alignments the procedure is basically:
Algorithm 1
1. Find the longest MUM (Maximal Unique Match) between the new version and the versions of the variant graph. 2. Merge the new version and the graph at that point, partitioning them both into two halves. 3. Call the algorithm recursively on the two subgraphs, each spanned by one segment of the new version.
Finding The Best MUM
When comparing two strings, a Maximal Exact Match, or MEM, is a sequence of consecutive matching characters in both strings that cannot be extended at either end. A MUM, or Maximal Unique Match, is a MEM that occurs only once in the two strings (Delc02). In Figure 11 ‘the quick brown fox’ and ‘ brown fox jumps over the ’ are both MUMs, while ‘the ’ is a MEM that also occurs elsewhere.
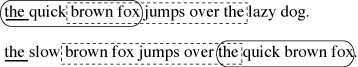
Figure 11: Maximal Exact Match and Maximal Unique Match
In the current problem MUMs will be sought between the new version being added to the graph and the entire graph, the longest of which is the best MUM. They need to be MUMs and not MEMs because otherwise erroneous alignments would be generated. For example, choosing arbitrary instances of multiple spaces at the start of lines, or repeated sequences of markup tokens as points of equivalence would lead to serious misalignments.
Finding the best MUM is related to the problem of finding the Longest Common Substring (LCS) between two strings. A naive approach to finding the LCS might look like this:
-
Examine each character in the first string and compare it with each character in the second string.
-
If the two characters are the same, continue comparing successive positions in the two strings until you get a mismatch.
-
Store the match in a table. If it was already present, increment its count by 1.
-
Once all characters in the first string have been used up, the best MUM is the longest string in the table whose frequency is 1.
Two problems with this naive approach are immediately clear: firstly it is inefficient, since it will take O(MN) time, where M and N are the lengths of the two strings. Secondly, the number of strings in the table will be enormous, as many as M2N2. A much faster and more space-efficient way is to use suffix trees.
A suffix tree stores all the suffixes of a given string. In Figure 12 each path from the root to a leaf spells out one possible suffix of ‘Woolloomooloo’. In the leaves are stored the start position of each suffix in the original string. A node labelled λ indicates that at this point in the tree a suffix occurs with no further text, e.g. for the suffixes ‘oo’ and ‘o’. A suffix tree can be used to find any substring of length M in that string with just M comparisons, however long the string may be.
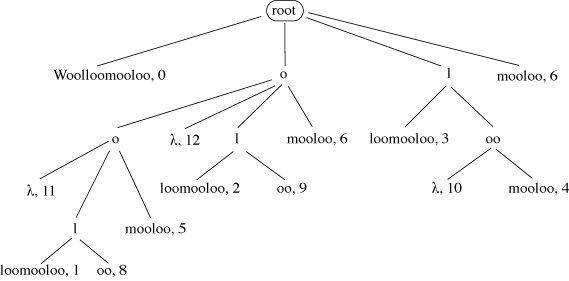
Figure 12: A Suffix Tree of ‘Woolloomooloo’
A suffix tree can be constructed in linear time using Ukkonen's algorithm (Ukko95). The LCS between two strings can also be calculated in linear time by building what is called a ‘generalised suffix tree’ (Gusf97, 125). A generalised suffix tree represents n strings instead of 1. For two strings this method constructs a suffix tree from one of the strings in linear time, then carries on building the same tree with the second string. The leaf nodes are labelled by the number of the string and the starting index in either or both strings. Any internal node that has only two leaves as children, one from each string, or any leaf shared by the two strings, must be the suffix of a MUM. The MUM itself can be recovered by counting backwards in both strings until a mismatch.
Unfortunately, it is unclear if one can build a suffix tree from a variant graph. How are the suffixes to be identified, and how can one represent starting offsets within arcs that belong to multiple versions? In any case the gains from using a generalised suffix tree appear to be minimal in practice, since its use greatly increases storage requirements.
The method adopted here resembles the streaming technique used in MUMmer (Delc02). In this method only one suffix tree is built. The other sequence is then streamed against it to find matches.
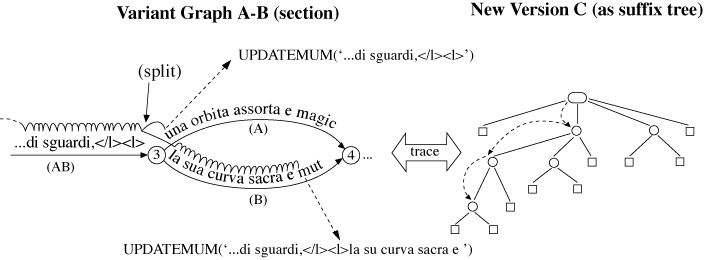
Figure 13: Finding Matches
The place of the streamed sequence can be taken by the variant graph, whose characters can be exhaustively listed by breadth-first traversal (Sedg88, 430f). Each successive character from the graph is traced in a suffix tree built from the text of the new version, as shown in Figure 13. At the end of an arc, for example, at node 3, MATCH calls itself recursively on each diverging arc until a mismatch occurs. At this point the MATCH procedure has detected a raw match, of which there are likely to be very many. Since all that is wanted is the longest MUM, some filtering of matches is clearly required.
-
Any match shorter than a minimum length (typically 3-5) can be discarded. The user, however, may set this to 1 for a finer-grained alignment.
-
Many matches are not unique in the suffix tree. Any match that terminates in an internal node shares a path with some other suffix in the tree, and can be discarded. This also cuts out most short matches that pass the first filter.
-
Most remaining matches are not maximal. This can be tested for by comparing the two characters immediately preceding the match in the new version and the variant graph. If they are the same, the match is not maximal and can be discarded.
Candidate MUMs surviving these tests are passed to the UPDATEMUM procedure. Experimental data suggests that, with a minimum match length of five, only about 15% of matches that make it through the three filters are not MUMs.
Time Complexity of the MATCH Procedure
The cost of scanning for matches between the graph and the new version is O(M(1+ )), where M is the number of characters in the graph, and
)), where M is the number of characters in the graph, and  the average length of a match in the suffix tree. In the case that the graph and
the new version have no characters in common, exactly M comparisons will be made.
On the other hand, in the worst case that the graph and the new version are identical,
the program will require NM/2 comparisons. So the time complexity lies between quadratic
and linear, depending on the number and distribution of differences between the graph
and the new version.
the average length of a match in the suffix tree. In the case that the graph and
the new version have no characters in common, exactly M comparisons will be made.
On the other hand, in the worst case that the graph and the new version are identical,
the program will require NM/2 comparisons. So the time complexity lies between quadratic
and linear, depending on the number and distribution of differences between the graph
and the new version.
Updating the MUM
The candidate MUMs, and their frequencies, are stored in a hashtable. When a new candidate MUM arrives from the MATCH procedure, and is already present in the table, its frequency is incremented, otherwise it is added to the table with frequency 1. After the scan of the variant graph is complete, the longest match in the table whose frequency is still 1 will be the best MUM. The cost of each update to the hashtable is constant, and the cost of the final searching through the entries to find the best MUM is an additional linear cost for the whole operation, which has no effect on the time complexity of the algorithm.
Merging the MUM into the Graph
Having found the longest MUM, the next step is to merge the new version with the variant graph at that point. In fact, before searching for the MUM the new version has already been added to the variant graph as a special arc connected to the start and end-nodes, as shown in Figure 14.

Figure 14: Direct Alignment, First Iteration
Definition 1
A special arc represents a new version as yet unassimilated into the variant graph, and is distinguished in some way from other non-special arcs. In all other respects a special arc is still part of the graph, and does not violate its definition because it is part of the unique path of the new version. In Figure 14 the C-arc is a special arc, and is drawn in grey to indicate its status. A special arc is associated with a MUM, which represents its best fit to the variant graph. In Figure 14 the longest MUM, marked in bold, is ‘</l><l>d’un antico acquedotto di sguardi,</l><l>la sua curva sacra e ’ (‘</l><l>of an ancient aqueduct of glances,</l><l>its curve sacred and ’), taken from the B-version. It can be merged with the rest of the variant graph by splitting the special arc and the graph at each end of the MUM, then adding new nodes as required, and finally connecting the new arcs to the right nodes. The result is shown in Figure 15.

Figure 15: Direct Alignment, Second Iteration
Figure 16 shows that there are now two subgraphs on either side of the newly aligned section, and two subarcs left over from the special arc. The terms ‘subarc’ and ‘subgraph’ need to be defined because they will be used in the discussion that follows.

Figure 16: Subgraphs and Subarcs
Definition 2
A subgraph refers to either the entire graph, minus any special arcs, or to any subgraph thereof that conforms to the definition of the variant graph. It has distinguished start and end-nodes and a set of versions over which it ranges.
Definition 3
A subarc is a special arc left over after the merging of another special arc. In Figure 16 ‘<l>Questa è la ultima porta’ and ‘solitaria:</l>’ are both subarcs.
Algorithm 1 can now be called on the subarcs and their corresponding subgraphs. This process of alignment and recursion will continue until the length of a subgraph or subarc falls below the minimum, or no further MUMs can be found. In Figure 16, the right subgraph and its subarc can be merged by the shared MUM ‘a:</l>’ and on the left by ‘<l>Questa è la ultima ’. Once those merges have been carried out, however, no further merges of more than one character are possible.
One Small Problem
In the subgraphs of Figure 16, the right subgraph no longer contains a complete A-version. Since the A and B versions on the right are not parallel, it is impossible to tell which portion of A corresponds to the remaining part of the C-version. This is not ideal and does lead to some misalignments. For example, if the text of version C had ended with ‘magic’ instead of ‘solitari’, then, after merging, ‘magic’ would occur twice in the graph, as shown in Figure 17. Order sensitivity has not been entirely banished, as in the POA algorithm.

Figure 17: A Non-optimal Alignment
One solution is to optimise the graph subsequently. Anomalies like these can be merged away by reconsidering all combinations of arcs between shared endpoints once the first pass of the algorithm has produced a rough version of the graph. In this way the two ‘magic’s could be identified as identical variants of one another and merged. In bioinformatics such iterative refinement techniques have produced high quality alignments, for example TCOFFEE (Notr00) DIALIGN (Morg96) and MAFFT (Kato02). However, this problem does not so often arise in practice, and its solution is left open for future work.
Adding Transpositions
The addition of transpositions adds some complications to the simple algorithm just described. This section investigates why it is necessary to compute them at all, rather than simply identify them manually. It also describes how transpositions can be distinguished from random alignments between versions, and how they can be efficiently computed by a slight extension to the direct alignment algorithm.
Why Detect Transpositions Automatically?
In texts written by the author evidence of actual transpositions could refute any computational heuristic. Figure 18 shows a clear case of transposition. What need could there be to calculate the presence of transpositions when their existence can be precisely verified in this way?

Figure 18: A Clear Case of Transposition
Firstly, even in manuscripts written by the author, the presence of a transposition may not always be immediately obvious. The author may choose to completely rewrite the sentence or to indicate the transposition by some other means, such as insertion and deletion, as in Figure 19.
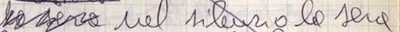
Figure 19: Deletion and Reinsertion of ‘la sera’
Secondly, in the case of multiple drafts, or multiple witnesses of the one text, the discovery of transpositions between physical versions is extremely difficult using any manual method. Even in the case of original manuscripts with corrections by the author, a good automatic method could produce the correct result most of the time. In that case, the editor would only be obliged to manually intervene in a small number of cases. Exactly how such a manual intervention would work is left for the moment as an open question.
What Constitutes a Transposition?
The edit cost of a transposition in biological sequences is considered to be constant, e.g. Lopresti and Tomkins (1997). If this was also true of documentary texts then even single characters that matched at the start and end of a long document would have to be considered as potential transpositions, but intuitively that isn’t likely.
A metric for assessing the validity of transpositions may instead be modelled as a threshold rather than as an edit cost. Whether a match is a transposition or not seems to be a function of the match's size and the distance between its two halves. Over what ranges those quantities of size and distance may vary can be determined by experiment.
A sample of 49 real cases of transposition were manually identified in a wide variety of texts:
The results are shown in Figure 20. ‘Size’ means the length of the transposed text and ‘distance’ is the distance in characters between the insertion and deletion points before the transposition was carried out.
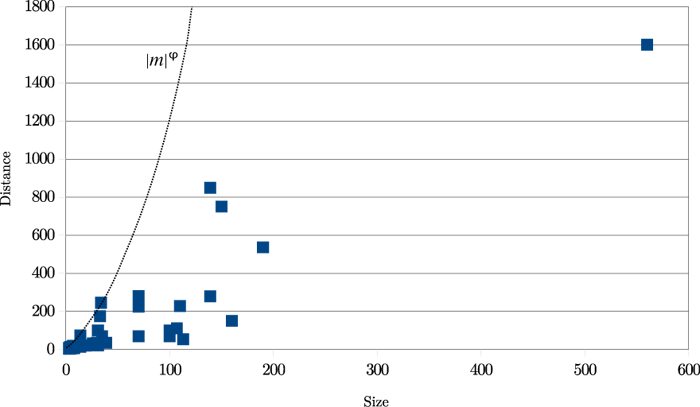
Figure 20: Transpositions: Size vs Distance
It is clear from this graph that real transpositions are mostly short-range affairs. (Not considered here are 'transpositions' produced by the reordering of entire works within a single manuscript, as in Spen03.) An approximate heuristic is d < |m|φ, where d is the distance between the two halves of the match, |m| its length, and φ is the golden ratio, approximately 1.618034. This ratio is relevant for two reasons: it has been used in the arts since classical times, particularly in architecture, and also it expresses a ratio of relative length: (a+b)/a = a/b = φ. All 49 examples meet this simple criterion. Using such a threshold yields the double benefit of decreasing the amount of calculation while increasing accuracy.
Merging Transpositions into the Variant Graph
Before describing the algorithm it is necessary to explain the difference between merging a direct alignment with the variant graph and merging a transposition. Conceptually a direct alignment and a transposition are very similar: both identify aligned parts in the new version and the variant graph, but in the transposition case the two halves of the alignment are not opposite one another.

Figure 21: Merging a Transposition
In Figure 21 ‘parrot’ has been identified as a transposition between versions B and C. Merging has been carried out so that the two instances of ‘parrot’ in versions B and C have been separated from their arcs by the addition of new nodes. This creates two new subarcs ‘the raucous’ and ‘swiftly’ on the left, which are both opposite the same subgraph ‘the dog’. The source instance ‘parrot’ in version B may still participate in further transpositions or even in a direct alignment, for example, if the C-version read ‘a surprised parrot’ instead of ‘a surprised lorikeet’. There is no harm in this, and in fact this is one way to detect repetitions. Apart from the addition of a node or two, merging a transposition does not materially change the structure of a variant graph. All that happens is that one half of the match is marked as the parent (in this case the B-version), and the other as the child (version C).
A Simple Algorithm for Detecting Transpositions
The place to look for transpositions of a special arc is thus anywhere except in its opposite subgraph and any arcs parallel to it. But in order to apply the threshold formula derived above to restrict the range of that search, there needs to be some accurate and reliable way to specify the distance between the two halves of a transposition. In Figure 22 the special arc, shown in grey, spans its subgraph, which is shown in the context of the overall graph. The special arc contains two matches, shown as thicker lines. The distance between the two halves of each match is measured backwards or forwards, following the shortest path, from the end of the match in the special arc to the start of the transposed text in the graph. The objective here is not to solve the shortest path problem optimally – in fact, the very idea of using a shortest path is itself a heuristic – but simply to provide a fast way to estimate distance. A simple breadth-first traversal combined with a greedy calculation of the shortest path to any node from its immediate predecessors provides the appropriate linear performance.

Figure 22: Measuring Transpose Distance
This measurement process also suggests an algorithm. To find what transpositions are possible for any special arc one only has to look to the left and right of the immediately opposite subgraph of a special arc, as far as the threshold formula allows. For any special arc A there is no point looking further than |A|φ bytes to the left or right. Of course, any match m that is found, where |m| < |A| also has to pass the threshold formula. Algorithm 2 uses this technique to modify Algorithm 1 to include transpositions, and also adds a bit more detail from the above discussion.
Algorithm 2
1. Set currentArc to a special arc made from the new version 2. Set currentGraph to the variant graph 3. Attach currentArc to the start and end of currentGraph 4. Compute the bestMUM between currentArc and currentGraph 5. Create a priority queue specials of tuples {Arc,MUM,Graph} 6. WHILE bestMUM is not NULL DO 7. Merge bestMUM into currentGraph. 8. FOR each subarc created by the merge DO 9. Compute the directMUM, leftTransposeMUM and rightTransposeMUM 10. Set MUM to the best of the three 11. IF MUM is not NULL THEN 12. Insert {subarc,MUM,subgraph} into specials; keep it sorted 13. END IF 14. END FOR 15. POP {currentArc, bestMUM, currentGraph} from specials; 16. END WHILE
Algorithm 2 creates a priority queue of triples Ai,Mi,Sj, where Ai is a special arc, Mi is its best MUM with the graph, and Sj is its opposite subgraph. It has a j subscript, not i because, as explained above, more than one special arc may share the same subgraph. The queue is kept sorted on decreasing length of MUM (line 12). In line 7 the longest MUM is used to create 0-2 new subgraphs and subarcs. Each new subarc, together with its subgraph and its best MUM, are added to the specials queue. When the queue no longer contains a valid MUM the program terminates.
The calculation of the two transpose MUMs uses the same process as the direct MUM, except that the variant graph is searched backwards on the left hand side from the start node of the subgraph, and forwards from its end node, as shown in Figure 22. The best such MUM found is recorded as the left or right transpose MUM for the special arc. In choosing the best of three in line 10, if a transpose MUM and a direct MUM are of the same length, the direct MUM is preferred.
This algorithm is admittedly naive, but it is easy to implement. In reality transpositions are often composed of imperfectly matched sections, that is, literal matches interspersed with small variants, deletions and insertions. Refinement of the algorithm to allow for such fuzzy matching is left for future work. For the moment, this simple atomic approach to transposition produces satisfactory results.
Time Complexity of Algorithm 2
There are three operations that have greater than constant cost:
-
Calculation of Direct Align MUMs (lines 4, 9). Since Algorithm 2 subdivides and recurses into smaller and smaller sections of the graph without recalculating MUMs except where a merge has been made, this process is essentially linear. The speed of the merge operation is thus governed by the cost of calculating the best MUM, which is O(MN).
-
Calculation of Transpose MUMs (line 9). The same observation applies to transpose MUMs, and its cost is likewise governed by the cost of computing the best MUM.
-
Keeping the specials Queue Sorted (line 12). Using a red-black tree the cost is only O(log Q), where Q is the queue length (Sedg88, 218f). This has no impact on the overall time complexity because it is always much cheaper than the cost of computing MUMs.
Thus, summing the direct alignment, transposition and sorting costs, the time complexity of merging one version into a variant graph using Algorithm 2, with block transpositions, is O(MN) in the worst case.
Experimental Performance of Algorithm 2
Algorithm 2 has been written up as a test program called MergeTester (http://www.itee.uq.edu.au/~schmidt/downloads.html), and has been run on a wide variety of multi-version example texts. The parameters measured are: author, title, average version size in kilobytes, number of versions, approximate date of manuscripts, total time to merge all versions in seconds and average time to merge one version after the first. Times were computed on a 1.66GHz processor. The test program was single-threaded.
Performance of Algorithm 2 on Example Texts
Table I
| Author | Title | Size | # Versions | Date | Total Time | Time Per Version |
|---|---|---|---|---|---|---|
| Galiano | El mapa de las aguas | 36.0 | 3 | 1993 | 8.0 | 4.0 |
| Chedid | La robe noire | 1.3 | 2 | 1996 | 0.2 | 0.2 |
| Bijns | Refrains | 15.4 | 3 | 16th C. | 5.0 | 2.5 |
| Huygens | Ooghentroost (fragment) | 3.4 | 6 | 17th C. | 2.0 | 0.4 |
| Cerami | La donna serpente | 12.0 | 9 | 1991 | 7.6 | 1.0 |
| Cerami | Le visioni del calvo | 12.0 | 5 | 1991 | 2.9 | 0.7 |
| Cerami | L'uovo di colombo | 12.0 | 8 | 1991 | 3.0 | 0.4 |
| Cerami | Nascosti tra la folla | 12.0 | 7 | 1991 | 4.9 | 0.8 |
| Cerami | Paul Newman | 10.0 | 8 | 1991 | 5.7 | 0.8 |
| Cerami | Una donna alta | 12.0 | 11 | 1991 | 16.3 | 1.5 |
| Magrelli | Campagna romana | 0.6 | 15 | 1981 | 0.8 | 0.05 |
| ANC Corpus | Adams Elissa | 3.4 | 5 | 20th C. | 7.0 | 1.7 |
| Anon | Sibylline Gospel | 3.0 | 36 | 4th-12th C. | 28.4 | 0.8 |
| Malvezzi | El Rómulo | 98.2 | 5 | 17th C. | 68.0 | 17.0 |
Alignment Quality
As pointed out in Darling et al. (Darl04, 1398), anchor-based alignment techniques that detect transpositions are very difficult to assess objectively. For multiple sequence alignment programs the manually aligned Baslibase archive (Thom99) has been used as a measure of alignment quality. No such benchmark also exists for texts aligned with transpositions and repeats. Visual inspection is subjective, very difficult, and likely to miss many errors. All that can be said at this stage is that, with the exception of the Malvezzi texts (see below), all of the alignments appear to be of good quality, with few missed transpositions or misalignments.
Conclusion
The problem of how to merge n versions of a text into a variant graph is closely related to applications in biology that seek to compare genetic or amino acid sequences. Their output has traditionally been either a set of aligned sequences or a phylogentic tree showing the interrelationships between versions. Transpositions were not considered.
Like the biologists, humanists have also developed programs to ‘collate’ or compare versions to find differences, originally with a view to constructing the apparatus criticus of the print edition (a kind of alignment), and also a stemma (a kind of phylogenetic tree). Recently they have also tried to apply biological techniques to their texts.
The biologists have recently realised the importance of transpositions, and have tried to create new methods for genome comparison that includes them. Some of these new techniques seek to replace the traditional matrix representation of a multiple sequence alignment by a directed graph. Their graph models, however, are much more complex than the variant graph, although they represent practically the same information. They are also very slow to construct if they attempt to align individual characters. None of the biological programs can be directly applied to the different requirements of humanities and linguistics multi-version texts.
The inclusion of transpositions renders the problem of calculating an optimal alignment between multiple versions intractable. But an optimal alignment is not really necessary. Instead, a heuristic method for aligning n versions with block transpositions has been described, which has O(MN) performance in the worst case, and is often much faster. It uses a novel technique for filtering transpositions via a simple threshold formula, which reduces the amount of computation while increasing accuracy. In texts of typical length of around 50K it can add or replace a version in a variant graph or multi-version document in a few seconds.
Although this represents a ‘first cut’ at solving a difficult problem, results are encouraging enough to demonstrate the viability of using variant graphs or MVDs to overcome the long-standing problems of how to represent ‘overlapping hierarchies’ and multiple versions in humanities texts.
Acknowledgements
This work, although independent research, is supported by the Italian project CoOPERARE (Content Organisation, Propagation, Evaluation and Reuse through Active Repositories), Project of Research in the National Interest (PRIN), 2008-09, whose Rome research unit is directed by Domenico Fiormonte.
The example texts of Angel Garcia Galiano, Vicenzo Cerami and Valerio Magrelli were provided by Digital Variants. The texts of Huygens and Anna Bijns were supplied by Ron Van den Branden of the CTB in Belgium. The Malvezzi texts were supplied by Carmen Isasi of the University of Deusto, Spain, and the Sibylline Gospel texts by Nicoletta Brocca of the University of Venice Ca' Foscari.
References
[Aldo00] Aldous, J.M. and Wilson, R.J. Graphs and Applications an Introductory Approach. London: Springer, 2000.
[Barn88] Barnard, D., Hayter, R., Karababa, M., Logan, G., McFadden, J. ‘SGML-Based Markup for Literary Texts: Two Problems and Some Solutions’, Computers and the Humanities. 22: 265-276, 1988. doi:https://doi.org/10.1007/BF00118602
[Bart06] Bart, P.R. ‘Experimental markup in a TEI-conformant setting’, Digital Medievalist, 2: 2006.http://www.digitalmedievalist.org/article.cfm?RecID=10"
[Boe08] Böe, H. ‘Manuscript Encoding Clarification and Transposition; New Features for the Module for Transcription of Primary Sources?’, unpublished. http://www.emunch.no/tei-mm-2008/index_ms.html
[Bour07] Bourdaillet, J. Alignment textuel monolingue avec recherche de déplacements: algorithmique pour la critique génétique. PhD Thesis, Université Paris 6 Pierre et Marie Curie, 2007.
[Bray03] Bray, N., Dubchak, I. and Pachter, L. AVID: A Global Alignment Program, Genome Research, 2003, 97-102.
[Bray08] Bray, T., Paoli, J., Sperberg-McQueen, C.M., Maler, E., Yergeau, F. Extensible Markup Language (XML) 1.0 (Fifth Edition). http://www.w3.org/TR/2008/PER-xml-20080205/
[Brud03a] Brudno, M., Do, C.B., Cooper, G.M., Kim, M.F., Davydov, E., Green, E.D., Sidow, A., Batzoglou, S. ‘LAGAN and Multi-LAGAN: Efficient Tools for Large-Scale Multiple Alignment of Genomic DNA’, Genome Research, 13: 721-731. doi:https://doi.org/10.1101/gr.926603
[Brud03b] Brudno, M., Malde, S., Poliakov, A., Do, C.B., Couronne, O., Dubchak, I. and Batzoglou, S. ‘Glocal alignment: finding rearrangements during alignment’, Bioinformatics, 19: 2003, 154-162. doi:https://doi.org/10.1093/bioinformatics/btg1005
[Buzz02] Buzzetti, D. ‘Digital Representation and the Text Model’, New Literary History, 33: 2002, 61-88. doi:https://doi.org/10.1353/nlh.2002.0003
[Darl04] Darling, A.C.E., Mau, B. and Blattner, F.R. Mauve: Multiple Alignment of Conserved Sequence With Rearrangements. Genome Research, 14: 2004, 1394-1403. doi:https://doi.org/10.1101/gr.2289704
[Debr46] de Bruijn, N.G. ‘A Combinatorial Problem’, Koninklijke Nederlandse Akademie v. Wetenschappen, 49: 1946, 758-764.
[Delc02] Delcher, A.L., Phillippy, A., Carlton, J. and Salzberg, S.L. ‘Fast algorithms for large-scale genome alignment and comparison’. Nucleic Acids Research, 30.11: 2002, 2478-2483. doi:https://doi.org/10.1093/nar/30.11.2478
[Dero04] DeRose, S. ‘Markup Overlap: A Review and a Horse,’ Extreme Markup Languages Conference, Montreal, 2004. http://www.idealliance.org/papers/extreme/proceedings/html/2004/DeRose01/EML2004DeRose01.html
[Edga06] Edgar, R.C. and Batzoglou, ‘Multiple sequence alignment’, Current Opinion in Structutural Biology, 16: 2006, 368-373. doi:https://doi.org/10.1016/j.sbi.2006.04.004
[Feng87] Feng, D.F. and Doolittle, R.F. ‘Progressive Sequence Alignment as a Prerequisite to Correct Phylogenic Trees’, Journal of Molecular Evolution, 25: 1987, 351-360. doi:https://doi.org/10.1007/BF02603120
[Frog68] Froger, D.J. La Critique des textes et son automatisation. Paris: Dunod, 1968.
[Gabl84] Gabler, H.W. ‘Towards an Electronic Edition of James Joyce's Ulysses’, Literary and Linguistic Computing, 15: 2000, 115-120. doi:https://doi.org/10.1093/llc/15.1.115
[Gare79] Garey, M.R. and Johnson, D. ‘Computers and Intractability; A Guide to the Theory of NP-Completeness’, San Francisco: Freeman, 1979.
[Gold90] Goldfarb, C. The SGML Handbook. Oxford: Oxford University Press, 1990.
[Good46] Good, I.J. ‘Normal Recurring Decimals’, Journal of the London Mathematical Society, 21: 1946, 167-169. doi:https://doi.org/10.1112/jlms/s1-21.3.167
[Gras04] Grasso, C. and Lee, C. ‘Combining partial order alignment and progressive multiple sequence alignment increases alignment speed and scalability to very large alignment problems’, Bioinformatics, 20.10: 2004, 1546-1556. doi:https://doi.org/10.1093/bioinformatics/bth126
[Gree94] Greetham, D.C. Textual Scholarship: An Introduction. New York and London: Garland, 1994.
[Gu99] Gu, Q-P., Peng, S. and Sudborough, H. ‘A 2-approximation algorithm for genome rearrangement by reversals and transpositions’, Theoretical Computer Science, 210: 1999, 327-339. doi:https://doi.org/10.1016/S0304-3975(98)00092-9
[Gusf97] Gusfield, D. Algorithms on Strings, Trees and Sequences: Computer Science and Computer Biology. Cambridge: Cambridge University Press, 1997.
[Guye97] Guyer, G.S., Heath, L.S., Vergara, J.P.C. ‘Subsequence and Run Heuristics for Sorting by Transpositions’, Technical Report TR-97-20, Virginia Polytechnic Institute and State University, 1997. http://historical.ncstrl.org/tr/fulltext/tr/vatech_cs/TR-97-20.txt
[Heck78] Heckel, P. ‘A Technique for Isolating Differences Between Files’, Communications of the ACM, 21.4: 1978, 264-268. doi:https://doi.org/10.1145/359460.359467
[Ide06] Ide, N. and Suderman, K. ‘Integrating Linguistic Resources: The American National Corpus Model’, Proceedings of the Fifth Language Resources and Evaluation Conference, 2006.
[Idur95] Idury, R.M. and Waterman, M.S. ‘A New Algorithm for DNA Sequence Assembly’, Journal of Computational Biology, 2.2: 1995, 291-306. doi:https://doi.org/10.1089/cmb.1995.2.291
[Kato02] Katoh, K., Misawa, K., Kuma, K. and Miyata, T. ‘MAFFT: a novel method for rapid multiple sequence alignment based on Fast Fourier transform’, Nucleic Acids Research, 30.14: 2002, 3059--3066. doi:https://doi.org/10.1093/nar/gkf436
[Lass02] Lassmann, T. and Sonnhammer, E.L.L. ‘Quality assessment of multiple alignment programs’, FEBS Letters, 529: 2002, 126-130. doi:https://doi.org/10.1016/S0014-5793(02)03189-7
[Lee02] Lee, C. Grasso, C. and Sharlow, M.F. ‘Multiple sequence alignment using partial order graphs’, Bioinformatics, 18.3: 2002, 452-464. doi:https://doi.org/10.1093/bioinformatics/18.3.452
[Lesk02] Lesk, A.M. Introduction to Bioinformatics. Oxford: Oxford University Press, 2002.
[Leve66] Levenshtein, V.I. ‘Binary Codes Capable of Correcting Insertions and Reversals’, Soviet Physics: ‘Doklady’, 10.8: 1966, 707-710.
[Lopr97] Lopresti, D. and Tomkins, A. ‘Block edit models for approximate string matching’, Theoretical Computer Science, 181: 1997, 159-179. doi:https://doi.org/10.1016/S0304-3975(96)00268-X
[Maas03] Maas, J.F. Vollautomatische Konvertierung mehrfach XML-annotierter Texte in das NITE-XML Austauschformat, Masters Dissertation, Uni. of Bielefeld, 2003. http://coli.lili.uni-bielefeld.de/Texttechnologie/Forschergruppe/sekimo/nite/Text/Magisterarbeit.pdf
[Magr81] Magrelli, V. Ora serrata retinae. Milan: Feltrinelli, 1981.
[Mcga01] McGann, J.J. Radiant Textuality. London: Palgrave McMillan, 2001.
[Mcga06] McGann, J.J. Juxta, 2006. http://www.patacriticism.org/juxta/
[Morg96] Morgenstern, B., Dress, A. and Werner, T. ‘Multiple DNA and Protein Sequence Alignment Based on Segment-To-Segment Comparison’, Proceedings of the Natioanl Academy of Sciences of the United States of America, 93.22: 1996, 12098-12103. doi:https://doi.org/10.1073/pnas.93.22.12098
[Need70] Needleman, S.B. and Wunsch, C.D. ‘A General Method Applicable to the Search for Similarities in the Amino Acid Sequence of Two Proteins’, Journal of Molecular Biology, 48: 1970, 443-453. doi:https://doi.org/10.1016/0022-2836(70)90057-4
[Nedo99] Nedo, M. Ludwig Wittgenstein Wiener Ausgabe Studien Texte Band 1-5. Vienna and New York: Springer, 1999.
[Neyt06] Neyt, V. ‘Fretful Tags Amid the Verbiage: Issues in the Representation of Modern Manuscript Material’, Literary and Linguistic Computing, 21: 2006, 99-111. doi:https://doi.org/10.1093/llc/fql002
[Notr00] Notredame, C, Higgins, D.G. and Heringa, J. T-Coffee: ‘A Novel Method for Fast and Accurate Multiple Sequence Alignment’, Journal of Molecular Biology, 302: 2000, 205-217. doi:https://doi.org/10.1006/jmbi.2000.4042
[Ott00] Ott, W. Stategies and Tools for Textual Scholarship: the Tübingen System of Text Processing Programs (TUSTEP)’, Literary and Linguistic Computing, 15.1: 2000, 93-108. doi:https://doi.org/10.1093/llc/15.1.93
[Page72] Page, D.L. Aeschyli Septem quae Supersunt Tragoedias. Oxford: Clarendon Press, 1972.
[Pevz89] Pevzner, P. ‘L-Tuple DNA sequencing. Computer Analysis’, Journal of Biomolecular Structure and Dynamics, 7: 1989, 63-73.
[Pevz01] Pevzer P.A., Tang, H. and Waterman, M.S. ‘An Eulerian path approach to DNA fragment assembly’, Proceedings of the National Academy of Sciences USA, 98.17: 2001, 9748-9753. doi:https://doi.org/10.1073/pnas.171285098
[Pevz04] Pevzner, P.A., Tang, H. and Tesler, G. ‘De Novo Repeat Classification and Fragment Assembly’. Genome Research, 14: 2004, 1786-1796. doi:https://doi.org/10.1101/gr.2395204
[Raph04] Raphael, B., Zhi, D. and Tang, H. ‘A novel method for multiple alignment of sequences with repeated and shuffled elements’, Genome Research, 14: 2004, 2336-2346. doi:https://doi.org/10.1101/gr.2657504
[Robi89] Robinson, P.M.W. ‘The Collation and Textual Criticism of Icelandic Manuscripts (1): Collation’, Literary and Linguistic Computing 4.2: 1989, 99-105. doi:https://doi.org/10.1093/llc/4.2.99
[Sahl05] Sahle, P. ‘Digitales Archiv – Digitale Edition. Anmerkungen zur Begriffsklärung’. In: Literatur und Literaturwissenschaft auf dem Weg zu den neuen Medien, M. Stoltz, L.M. Gisi and J. Loop (eds), Basel: germanistik.ch, 2005.
[Schm08] Schmidt, D., Brocca, N. and Fiormonte, D. ‘A Multi-Version Wiki’. In: Proceedings of Digital Humanities 2008, Oulu, Finland, June, E.S. Ore and L.L. Opas-Hänninen (eds), 187-188.
[Schm09] Schmidt, D. and Colomb, R. ‘A data structure for representing multi-version texts online’. International Journal of Human-Computer Studies. 67.6: 2009, 497-514. doi:https://doi.org/10.1016/j.ijhcs.2009.02.001.
[Schw00] Schwartz, S., Zhang, Z. and Frazer, A. ‘PipMaker A Web Server for Aligning Two Genomic DNA Sequences’, Genome Research, 10: 2000, 577-586. doi:https://doi.org/10.1101/gr.10.4.577
[Sedg88] Sedgewick, R. Algorithms. Reading Massachusetts: Addison-Wesley, 1988.
[Shap02] Shapira, D. and Storer, D.A. ‘Edit Distance with Move Operations’, Lecture Notes in Computer Science, 2373: 2002, 85-98. doi:https://doi.org/10.1007/3-540-45452-7_9
[Shil96] Shillingsburg, P.L. Scholarly Editing in the Computer Age. Theory and Practice. AnnArbor: University of Michigan Press, 1996.
[Spen04] Spencer, M. and Howe, C.J. ‘Collating Texts Using Progressive Multiple Alignment’, Computers and the Humanities, 38: 2004, 253-270. doi:https://doi.org/10.1007/s10579-004-8682-1
[Spen03] Spencer, M. Bordalejo, B., Wang, Li-San, Barbrook, A.C., Mooney, L.R., Robinson, P., Warnow, T and Howe, C.J. ‘Analyzing the Order of Items in Manuscripts of The Canterbury Tales’, Computers and the Humanities, 37.1: 2003, 97-109. doi:https://doi.org/10.1023/A:1021818600001
[Stuh08] Stührenberg, M. and Goecke, D. ‘SGF - An integrated model for multiple annotations and its application in a linguistic domain’. In: Balisage: The Markup Conference Proceedings. http://www.balisage.net/Proceedings/vol1/html/Stuehrenberg01/BalisageVol1-Stuehrenberg01.html. doi:https://doi.org/10.4242/BalisageVol1.Stuehrenberg01
[Thom94] Thompson, J.D., Higgins, D.G. and Gibson, T.J. ‘CLUSTALW: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice’. Nucleic Acids Research, 22: 1994, 4673-4680. doi:https://doi.org/10.1093/nar/22.22.4673
[Thom99] Thompson, J.D., Plewniak, F. and Poch, O. BAliBASE: a benchmark alignment database for the evaluation of multiple alignment programs, Bioinformatics, 15: 1999, 87-88. doi:https://doi.org/10.1093/bioinformatics/15.1.87
[Tich84] Tichy, W.F. ‘The String-to-String Correction Problem with Block Moves’, ACM Transactions on Computer Systems 2.4: 1984, 309-321. doi:https://doi.org/10.1145/357401.357404
[Ukko95] Ukkonen, E. ‘On-Line Construction of Suffix Trees’, Algorithmica, 14: 1995, 249-260. doi:https://doi.org/10.1007/BF01206331
[Vand08] Van den Branden, R. ‘A Modest Proposal. Analysis of Specific Needs with Reference to Collation in Electronic Editions’, Digital Humanities 2008 University of Oulu, June 24-29 Book of Abstracts, 2008, 206-207.
[Vett03] Vetter, L. and McDonald, J. ‘Witnessing Dickinson’s Witnesses’, Literary and Linguistic Computing, 18.2: 2003, 151-165. doi:https://doi.org/10.1093/llc/18.2.151
[Wagn75] Wagner, R.A. ‘On the Complexity of the Extended String-to-String Correction Problem’. In: Annual ACM Symposium on Theory of Computing. Proceedings of seventh annual ACM symposium on Theory of computing, A.K. Chandra, A.R. Meyer, W.C. Rounds, R.E. Stearns, R.E. Tarjan, S. Winograd, P.R. Young (eds), 1975, 218-223. doi:https://doi.org/10.1145/800116.803771
[Witt02] Witt, A. Multiple Informationsstrukturierung mit Auszeichnungssprachen. XML-basierte Methoden und deren Nutzen für die Sprachtechnologie, PhD Dissertation, Uni. of Bielefeld, 2002. http://deposit.ddb.de/cgi-bin/dokserv?idn=963909436