How to cite this paper
Marcoux, Yves, Michael Sperberg-McQueen and Claus Huitfeldt. “Modeling overlapping structures: Graphs and serializability.” Presented at Balisage: The Markup Conference 2013, Montréal, Canada, August 6 - 9, 2013. In Proceedings of Balisage: The Markup Conference 2013. Balisage Series on Markup Technologies, vol. 10 (2013). https://doi.org/10.4242/BalisageVol10.Marcoux01.
Balisage: The Markup Conference 2013
August 6 - 9, 2013
Balisage Paper: Modeling overlapping structures
Graphs and serializability
Yves Marcoux
Associate professor
Université de Montréal, Canada
Michael Sperberg-McQueen
Senior consultant
Black Mesa
Technologies
Claus Huitfeldt
Associate professor
University of Bergen, Norway
Copyright © 2013 by the authors. Used with permission.
Abstract
The problem of overlapping structures has long been familiar to the
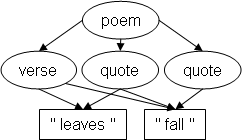
structured document community. In a poem, for example, the verse and line
structures overlap, and having them both available simultaneously is
convenient, and sometimes necessary (for example for automatic analyses).
However, only structures that embed nicely can be represented directly in
XML. Proposals to address this problem include XML solutions (based
essentially on a layer of semantics) and non-XML ones. Among the latter is
TexMecs HS2003, a markup language that allows overlap
(and many other features).
XML documents, when viewed as graphs, correspond to trees. Marcoux M2008 characterized overlap-only TexMecs documents by
showing that they correspond exactly to completion-acyclic node-ordered directed acyclic graphs.
In this paper, we elaborate on that result in two ways.
First, we cast it in the setting of a strictly larger class of graphs,
child-arc-ordered directed graphs, that
includes multi-graphs and non-acyclic graphs, and show that —
somewhat surprisingly — it does not hold in general for graphs with
multiple roots. Second, we formulate a stronger condition, full-completion-acyclicity, that guarantees
correspondence with an overlap-only document, even for graphs that have
multiple roots.
The definition of fully-completion-acyclic graph does not in itself
suggest an efficient algorithm for checking the condition, nor for
computing a corresponding overlap-only document when the condition is
satisfied. We present basic polynomial-time upper bounds on the complexity
of accomplishing those tasks.
Table of Contents
- 1. Motivation and related work
-
- 1.1. Graphs and documents
- 1.2. The problem of serialization
- 1.3 The approach of this paper
- 2. Child-arc-ordered directed graphs
- 3. Overlap-only documents
- 4. Correspondence between a graph and a document
- 5. Main results
- 6. Checking full-completion-acyclicity
- 7. Conclusion and future work
- Appendix A. Notation and symbols
1. Motivation and related work
1.1. Graphs and documents
Many operations are more conveniently performed on a graph
representation than on a linear representation of a marked up
document, and vice versa. One of the strengths of XML is that
XML documents in serial form are readily deserialized into
ordered trees, which form a convenient data structure for many
useful operations.
So-called “XML trees” are directed acyclic
graphs with single parenthood and a total ordering on leaf
nodes. While this constitutes an intuitively natural and
generally suitable model for the representation of the
structure of most documents, and for most purposes, it also
poses a challenge for the representation of complex structures
such as overlapping, fragmented or disordered document
elements, and multiple co-existing alternative structures,
which allow for a more natural representation of complex
documents in a wide range of situations.
For such purposes, a different kind of graph
representation has been proposed, the so-called Goddag SH2004. Roughly, Goddags (General Ordered-Descendant Directed Acyclic
Graphs) are like XML trees except that they allow
multiple parenthood and do not require a total ordering on
leaf nodes. (Thus, XML trees constitute a subset of
Goddags.)
Documents using different techniques for representing such
structures in XML form (e.g., milestones, fragmentation,
virtual elements, etc. B1995 SH1999 W2005) can be mapped onto
Goddags, though not without application-specific mechanisms
typically involving levels of indirection which may appear
cumbersome. The experimental markup system TexMecs HS2003 offers mechanisms for the representation of
complex structures which can be mapped on to Goddags
independently of such knowledge.
Since its introduction, the Goddag data structure has
frequently been cited, and it is used as a reference in
various works on overlap. (For example, Moore M2012
studied Goddags in the context of access control, and
introduced the notion of globally ordered
Goddag.) However, the original description of
Goddags is rather informal, and exhibits the kinds of gaps,
vaguenesses, and ambiguities that have, over time, given
informality a bad name among mathematicians and others
interested in firm results.
For example, it was conjectured that a
linearized document which made use, in addition to the
mechanisms of XML, only of markup for overlapping elements,
could be represented by a Goddag with a total order on leaf
nodes (so-called restricted
Goddags), but no proofs were given of this fact. The paper was
silent and its authors agnostic about the serializability of
graphs with multiple roots, and the relationship between Goddags
and markup in terms of serializability was not systematically
investigated. In HS2003, it was assumed, but
no attempt was made to prove, that all TexMecs documents could
be represented as Goddags, or that all Goddags could be
serialized as TexMecs documents. The present paper is a modest
contribution towards straightening up the situation, by way of a
systematic study of the fine point of the complex relationship
between markup formalisms like TexMecs and graph structures like
Goddags.
1.2. The problem of serialization
The general problem is this: whenever a markup system (be it
XML, TexMecs, or another system) provides more than one way to
represent a given abstract structure,
that same abstract structure can be written out again
(serialized) in more than one way. Can we control the
serialization process to provide the marked-up forms we find
easiest to work with at a given moment? Can we tell, by
inspection of a given graph, what serialization formats are
possible for the graph? In many cases, a marked up form using
overlapping elements, seems to at least some observers to be the
most natural
representation of a given document;
when can a graph be serialized using overlap alone, and when
does it require use of the more powerful mechanisms of virtual
or discontinuous elements?
A concrete example may help illustrate the point.
In the following fragment (adapted from D2004), the verse elements are
empty milestones marking the beginning and end of verses, in
Trojan Horse
style markup. A Goddag structure
representing this fragment would have nodes for the verses,
but those nodes do not correspond one to one with XML elements
in this serialization:
<div xmlns="http://www.tei-c.org/ns/1.0">
<p>
<verse xml:id="Jer.2.1"/>
Moreover the word of the LORD
came to me, saying,
<verse eID="#Jer.2.1"/>
<q n="Q-Jer.2.2-A">
<verse xml:id="Jer.2.2"/>
Go and cry in the
hearing of Jerusalem, saying,
<q n="Q-Jer.2.2-B">
Thus says the LORD:
<q n="Q-Jer.2.2-C">
I remember you,
The kindness of your youth,
The love of your betrothal,
When you went after Me in the wilderness,
In a land not sown.
<verse eID="#Jer.2.2"/>
<verse xml:id="Jer.2.3"/>
Israel [was] holiness to the LORD,
The firstfruits of His increase.
All that devour him will offend;
Disaster will come upon them,
</q>
<!--True Close Q-Jer.2.2-C-->
says the LORD.</q>
<verse eID="#Jer.2.3"/>
<!--* ... *-->
</q>
</p>
</div>
The same Goddag structure can also be serialized in an extended
form of TexMecs notation.
<div|
<p|
<verse@Jer.2.1|Moreover the word
of the LORD came to me, saying,|verse>
<q n="Q-Jer.2.2-A"|
<verse@Jer.2.2|
Go and cry in the
hearing of Jerusalem, saying,
<~@Jer.2.2b|
Thus says the LORD:|~>
<~@Jer.2.2c|
I remember you,
The kindness of your youth,
The love of your betrothal,
When you went after Me in the wilderness,
In a land not sown.|~>
|verse>
<q n="Q-Jer.2.2-B"|
<=@Jer.2.2b=>
<q n="Q-Jer.2.2-C"|
<=Jer.2.2c=>
<~@Jer.2.3a|
Israel [was] holiness to the LORD,
The firstfruits of His increase.
All that devour him will offend;
Disaster will come upon them,
|~>
|q>
|q>
<verse@Jer.2.3|
<=Jer.2.3a=>
says the LORD.
|verse>
<* ... *>
|q>
|p>
|div>
This particular Goddag structure can also be
serialized without virtual elements, just by allowing
the q and verse elements
to overlap:
<div|
<p|
<verse@Jer.2.1|
Moreover the word of the LORD
came to me, saying,
|verse>
<q n="Q-Jer.2.2-A"|
<verse@Jer.2.2|
Go and cry in the
hearing of Jerusalem, saying,
<q n="Q-Jer.2.2-B"|
Thus says the LORD:
<q n="Q-Jer.2.2-C"|
I remember you,
The kindness of your youth,
The love of your betrothal,
When you went after Me in the wilderness,
In a land not sown.
|verse>
<verse@Jer.2.3|
Israel [was] holiness to the LORD,
The firstfruits of His increase.
All that devour him will offend;
Disaster will come upon them,
|q>
says the LORD.
|verse>
|q>
<* ... etc. ... *>
|q>
|p>
|div>
Intuitively, many readers find the overlap-only version of the
document simpler and more natural than the version using
bilocation tags. But (as demonstrated by
M2008), not all Goddag structures can be
written out using only overlap, without virtual elements,
discontinuous elements, or bilocation tags.
This leads directly and obviously to the questions
When can graphs be serialized
using overlap only? And conversely, when are other
markup mechanisms necessary?
Marcoux M2008 introduced the notions of
noDAG and overlap-only
(oo) TexMecs as a first step towards answering these
questions.
A noDAG is a node-ordered directed acyclic graph,
i.e., a slight variation on the Goddag, where there is a strict partial
ordering on nodes. As a markup language, oo-TexMecs is the subset of TexMecs that
allows multiple roots and overlapping elements, but not virtual or interrupted
elements. Marcoux established that a noDAG is serializable if and only if it is
completion-acyclic, and that
“round-tripping” is possible, in that there is essentially a
bijective correspondence between noDAGs and oo-TexMecs documents.
1.3 The approach of this paper
In order to investigate whether and how the results of
M2008 apply to other classes
of graphs, we introduce here the more general notion of a child-arc-ordered directed graph (CODG), and
demonstrate that the results from M2008 hold also for CODGs,
with the somewhat surprising exception of some CODGs with multiple roots. By defining the stronger
notion of “fully completion-acyclic” graphs, we succeed in
identifying this subset: the oo-serializable CODGs are exactly the
fully-completion-acyclic ones. We also give basic polynomial-time upper bounds
on the complexity of checking full-completion-acyclicity and of actually
computing an oo-serialization of fully-completion-acyclic
CODGs.
2. Child-arc-ordered directed graphs
2.1 Definition A child-arc-ordered directed graph (CODG for short) G = (V, ch) is a
directed graph over a
finite
non-empty set of vertices (or nodes) V, where ch (for children) is a total mapping from V to finite (and possibly
empty) sequences of nodes from V. The set of arcs (or edges) of G, noted
E(G), comprises exactly those ordered pairs (v, w) for which
(∃n ∈ N)[ ch(v, n) = w ],
where N represents the set of non-negative integers. The notation
ch(v, n) is used as a shorthand for (ch(v))(n), that is, for the element with
index n in the sequence ch(v). We use 0-origin indexing; thus, for all v
∈ V, ch(v, 0) denotes the first child of v (or is undefined, if v has no child).
Note: Throughout this paper, the
“parent” relation must be understood to be the exact inverse of
the “child” relation (we bother to make this explicit because it
is not the case in some other models, such as
the XPath 1.0 data model).
It is possible for the same child to show up at more than one place
in a sequence of children; that is, ch(v, n) = ch(v, m) with m ≠ n is
possible. Loops are allowed; that is, ch(v, n) = v for a given n is possible.
Note that (v, w) ∈ E(G) for given v and w tells only part of the story: There
could be many distinct values of n for which ch(v, n) = w. Also note that the
length of ch(v), i.e., the smallest value of n (≥ 0) for which ch(v, n) is undefined,
is greater than or equal to the number of distinct children of v (if v has no child,
ch(v) = ∅, which, as a sequence, is of length 0).
CODGs are very loose structures: they can be
“multi-graphs,” in that more than one arc can link any given
pair of nodes. They can have cycles and loops (i.e., cycles of length one).
There can be both a direct (length one) and indirect path between any two given
nodes.
The rationale for the adjective child-arc-ordered
is that for all
v ∈ V, ch(v) can be seen as inducing an ordering on the arcs going out of
v (the
child-arcs
of v).
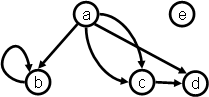
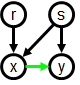
Examples We present examples of
CODGs illustrating some of their features.
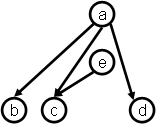
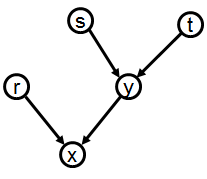
Example 2.1 illustrates that CODGs can be disconnected, and that, in a
CODG:
-
A node can have more than one parent (here most simply
node d, with parents a and c, but also node b [with
parents a and b]). This is a significant departure from
the rule of single parenthood in XML.
-
There can be cycles and loops (cycles of length 1); here
the only example is the loop on node b.
-
The same node can occur more than once as a child of
some parent (here node c, which is both second and fourth
among the children of node a).
-
There can be both direct and indirect paths between two
nodes (here node a dominates node d both directly and
via node c).
Note that the order of the
outgoing arcs is usually not shown explicitly in the visual representation of a CODG.
We adopt the convention of drawing
the arcs going out of any node in order from left to right (even if
the arcs must cross each other further down, in order to reach
the child node they point to). So the leftmost arc leaving any
parent is pointing to that parent's first child, and the
rightmost arc points to that parent's last child.
Thus, in Example 1, ch(a) = (b, c, d, c).
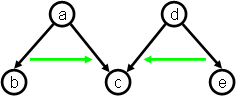
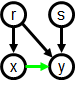
On the rare occasions that this convention is not practical, we use
explicit green arrows between the outgoing
arcs to indicate their order, as in the next example.
In Example 2.2, ch(a) = (b, c) and ch(d) = (e, c). Right-pointing
arrows, though superfluous, are sometimes shown as a reminder of the implicit
convention.
Sibling precedence For all v, ch(v)
induces a sibling-precedence
relation sp(v) among
the children of v, defined by:
sp(v) =def { (w, x) ∈ V × V
| (∃m, n ∈ N)[ m < n & ch(v, m) = w & ch(v, n) = x ]
}.
This relation may or may not be a strict order relation. When it is, we say that v
orders its children.
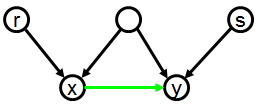
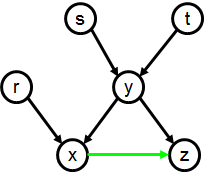
Example 2.3 illustrates that parents may order the same nodes
differently as children. Thus, note that ch(a) = (b, c), which induces the
strict order relation b
< c, and ch(d) = (c, b), which induces the strict order relation c < b.
In examples in which no pair of nodes is ordered differently by different
parents, we will usually place the green arrows between nodes, rather than between
arcs:
Auxiliary concepts We now define a
number of auxiliary concepts useful in discussions of CODGs. All
of them are secondary concepts in the sense that they are entirely and uniquely
determined by the set of vertices and the sequences of children of the
graph.
2.2 Definition Let G = (V, ch) be a
CODG. Then:
-
⇒G denotes the (positive)
transitive closure of E(G).
Note that ⇒G is not necessarily
antireflexive, as E(G) may contain cycles.
-
⇒*G
denotes the reflexive transitive closure of E(G), that is:
-
sp(G) =def { (v, w, x) ∈ V × V × V
| (∃m, n ∈ N)[ m < n & ch(v, m) = w & ch(v, n) = x ]
}.
The name “sp” stands for “sibling
precedence.” Note that, iff w occurs more than once in the sequence of
children of v, then (v, w, w) ∈ sp(G). Note also that it is entirely
possible for both (v, w, x) and and (v, x, w) to be members of sp(G).
Finally note that sp(G) is the union over all v ∈ V of ({v} × sp(v)),
where sp(v) is the sibling-precedence relation induced by ch(v), as defined above
at Sibling precedence.
-
gsp(G) =def { (w, x) ∈ V × V |
(∃v ∈ V)[ (v, w, x) ∈ sp(G) ] }.
The name “gsp” stands for “global sibling
precedence.” It is the projection of sp(G) onto the last two components.
It follows from the observations in the preceding point that there can be loops
and cycles in gsp(G).
2.3 Notation Let G = (V, ch) be a CODG.
Unless otherwise stated:
-
V can also be denoted by V(G),
-
E denotes E(G),
-
⇒ denotes ⇒G,
-
⇒* denotes
⇒*G,
-
sp denotes sp(G),
-
gsp denotes gsp(G).
3. Overlap-only documents
The phenomenon we wish to study in this paper is how the structural
properties of a CODG relate to the fact that it mimics the containment and
precedence relationships among elements in some marked-up document. More
specifically, we want to consider documents expressed in markup languages that
allow overlapping elements, such as TexMecs HS2003. Thus, we
need to define a model for such documents.
TexMecs allows many more constructs than element embedding and
overlap. However, in this paper, we concentrate on those two, ignoring the
others, such as virtual elements, interrupted elements, empty elements,
attribute specifications, entity references, generic identifier co-indexing
(for handling self-overlap), unordered contents, and comments. This is why we
speak of “overlap-only” (or “oo”) documents. When
the structure of a CODG corresponds to the containment and precedence
relationships of some oo-document (to be defined precisely in a moment), we say
the CODG is “oo-serializable,” because the oo-document can be
viewed as a serialization (a representation in
serial form) of the CODG.
Instead of defining documents as character strings with syntactic
constraints, we use a more abstract approach that avoids some complications and
leads to results that are simpler to formulate. More constraints on the
definition of document could later be added to suit specific markup languages
if and when desired.
Intuitively, we adopt a tokenized view of the document, where tokens
are tags and leaves. Tokens are represented by their (integer) position in the
sequence of tokens that make up the document.
The tags in our model of oo-documents correspond, in the XML
world, to start- and end-tags for non-empty elements.
The leaves in our model of oo-documents correspond, in the
XML world, to text nodes (#PCDATA) and empty elements. Note that
our model abstracts away from the actual textual content of
elements and documents, and also ignores the differences among
different element types. We claim, however, that our abstraction
captures the essential structural aspects of marked-up documents
with possible element overlap.
3.1 Definition An oo-document is a finite set of pairs of
the form (x, y), where x, y ∈ N (the set of non-negative
natural numbers) and x ≤ y, additionally satisfying a number of
“well-formedness” constraints (stated below).
The pairs in a document are called ranges. If r = (x, y) is a
range, then r1 and r2 denote
respectively x and y.
Intuitively, a range gives the position of a start-tag and of the
corresponding end-tag, or the position of a leaf, in which case, x =
y. Formally, if D is an oo-document:
-
leaves(D) =def { x ∈ N | (x, x)
∈ D },
-
stags(D) =def domain(D) -
leaves(D),
-
etags(D) =def image(D) -
leaves(D).
Note that, as usual:
-
domain(D) =def { x ∈ N | ( ∃ y ∈ N | (x,
y) ∈ D ) }, and
-
image(D) =def { y ∈ N | ( ∃ x ∈ N | (x,
y) ∈ D ) }, and
Oo-documents are subject to the following well-formedness
constraints.
For all oo-document D:
-
D is a partial function over N, i.e., for all x ∈ N,
there is at most one y such that (x, y) ∈ D.
-
D-1 (that is, the inverse
of D) is also a partial function over N, i.e., for all y
∈ N, there is at most one x such that (x, y)
∈ D.
-
stags(D) ∩ etags(D) = ∅.
Put less formally: No token is both a start-tag and an
end-tag.
It must also be remembered that (as stated at the beginning of the
definition) for all range r, r1 ≤
r2, which corresponds to the normal
rule of syntax that start-tag must precede its matching end-tag.
Note that we do not require the numbering of token positions to be
gap-free, nor do we forbid consecutive leaves without intervening
tags. There is also no requirement of an element spanning the whole
document: this is of course crucial for oo-documents to be able to
correspond to graphs with multiple roots.
3.2 Definition Let D be an oo-document,
and r, s ∈ D:
Note that in the latter case, r and s may or may not overlap. Also
note that r cannot both contain and precede
s.
4. Correspondence between a graph and a document
Intuitively, a CODG and an oo-document correspond to each other when the nodes of the graph and
the ranges of the document can be put in correspondence in such a way that node
reachability corresponds to range containment, and gsp corresponds to range
precedence.
4.1 Definition A CODG G and an
oo-document D correspond to each other iff
there exists a bijective mapping g from V(G) to D, such that all of the
following conditions hold:
-
(∀ b, c ∈ V(G)) [(b ⇒ c) iff g(b) contains
g(c)]
-
(∀ b, c ∈ V(G)) [if (b, c) ∈ gsp(G), then
g(b) precedes g(c)]
We then say that G and D correspond to each other
through g.
4.2 Definition A CODG G is said to
be oo-serializable iff there exists an
oo-document that corresponds to G.
It is clear that every oo-document has a corresponding CODG: use
ranges as nodes, and the transitive reduction of range containment as
parent-child relation. Then, order all sets of siblings in range precedence
order.
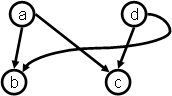
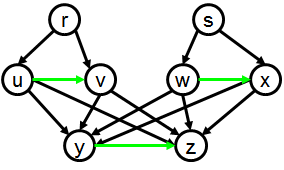
It is also clear that some CODGs are
not oo-serializable: for example, a CODG with cycles would imply (by
transitivity) a range containing itself, which is impossible. But are all
acyclic CODGs oo-serializable? The following examples, inspired from
M2008, show that the question is at best not trivial:
Both graphs are acyclic and they differ by just the presence/absence
of one arc. Yet, only the first one is oo-serializable M2008.
In M2008, Marcoux defined noDAGs, or
node-ordered DAGs, as (essentially) directed
acyclic graphs (DAGs) in which the nodes are partially ordered in such a way
that siblings (children of a common parent), as well as
distinct roots, are totally ordered. He then defined the property of
completion-acyclicity for noDAGs, and showed
that oo-serializable noDAGs are exactly the completion-acyclic ones.
In order to investigate whether the same is true of CODGs, we must
define an analogous property for CODGs. The following definition is the natural
adaptation of completion-acyclicity to CODGs.
4.3 Definition Let G = (V, ch) be a
CODG. Then:
-
ssba(G) =def { (w, x) ∈ V × V |
(∃v ∈ V)[ v ⇒ w & (v, x) ∈ gsp & x
⇏ w ] }.
The name “ssba” stands for
“should-start-before additions.”
-
ssb(G) denotes the transitive closure of (E ∪ gsp ∪
ssba).
The relation “ssb” is called the
“should-start-before completion” of G.
-
seaa(G) =def { (w, x) ∈ V × V |
(∃v ∈ V)[ v ⇒ w & (v, x) ∈
gsp-1 & x ⇏ w
] }.
The name “seaa” stands for “should-end-after
additions.” The relation gsp-1 is
the inverse of relation gsp.
-
sea(G) denotes the transitive closure of (E ∪
gsp-1 ∪ seaa).
The relation “sea” is called the
“should-end-after completion” of G.
4.4 Notation Let G = (V, ch) be a CODG.
Unless otherwise stated:
-
ssba denotes ssba(G),
-
ssb denotes ssb(G),
-
seaa denotes seaa(G),
-
sea denotes sea(G).
The relations ssb and sea can be understood as meaning:
“should <something>
in any oo-serialization of the
CODG,” for example “should
end after in any oo-serialization of the
CODG.” Thus, “(v, w) ∈ ssb” can be read out as:
“v should start before w in any oo-serialization of the CODG.” In
other words, ssb (respectively, sea) represents the start- (respectively, end-)
tag-precedence relations that can be deduced from the topology of the CODG,
supposing parent-child relations are interpreted as element containment, and
sibling-precedence relations as start- and end-tag-precedence.
The relations ssba and seaa represent the “additional”
arcs (over and above those in E and gsp or gsp-1)
that must be considered to compute all the
possible ssb and sea pairs that can be deduced from the CODG topology.
4.5 Definition A CODG G = (V, ch) is
said to be completion-acyclic (CA) iff each of
ssb(G) and sea(G) is acyclic.
5. Main results
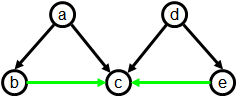
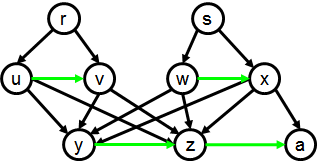
Things are not as simple with CODGs as with noDAGs. There
are, it turns out, CODGs that are completion-acyclic, yet not oo-serializable. Our
first result is to show that Example 2.2 above, as well as the following CODG,
are in that situation:
Since the number of structurally distinct documents that can
possibly correspond to a 5-node graph is finite, we could
exhaustively enumerate them and verify that none of them correspond
to either Example 2.2 or to
Example 6.
However, that would not be very
insightful.
We will thus rather proceed by way of a lemma (5.9) that
provides a general characterization of oo-serializable CODGs, and
will be useful for our second main result.
5.1 Definition Let G = (V, ch) be a
CODG. The ancestral precedence relation of G,
denoted ap(G), is defined as:
ap(G) =def { (v, w) ∈ V × V | (v
⇒ w) & (w ⇏ v) }.
It is easy to show that ap(G) is always a strict partial-order on V.
Informally, we could say that ap(G) gets rid of the cycles in G by contracting
its (maximal) strongly-connected components, then re-expanding them to an equal
number of disconnected
vertices.
5.2 Definition Let G = (V, ch) be a
CODG. A root in G is a vertex r ∈ V for
which:
(∄w ∈ V)[ (w, r) ∈ ap(G) ].
5.3 Notation Let G = (V, ch) be a CODG.
Unless otherwise stated, ap denotes ap(G).
The next result establishes that for any distinct roots v and w,
either v and w are in the same strongly-connected component, or else v and w
are unordered in each of ssb and sea.
5.4 Lemma Let G = (V, ch) be a CODG,
and v and w two distinct roots in G. Then, either:
or
{ (v, w), (w, v) } ∩ ((ssb ∪ sea) − ⇒) = ∅.
Note: For space consideration, most
proofs are omitted.
Thus, an important difference between noDAGs and CODGs is that the
latter can have unordered root pairs, whereas noDAGs have (by definition) their
roots totally-ordered.
5.5 Definition A CODG G = (V, ch) is
said to be sp-consistent iff gsp is an acyclic
relation, i.e., iff:
(∀v ∈ V)[(v, v) ∉ transitive-closure(gsp)].
Note that if G is truly a multi-graph, i.e., if some node occurs more
than once as a child of the same parent, then G is certainly
not sp-consistent. However, G could fail to be
sp-consistent without being a true multi-graph, for example if two siblings are
ordered differently by two distinct parents.
5.6 Definition A CODG G = (V, ch) is
said to be reduced iff no node is both
directly and indirectly reachable from some other node, i.e., iff:
(∄v, w, x ∈ V)[ {(v, w), (v, x)} ⊆ E(G) &
w ⇒ x].
Note that if there is a cycle in G, then it is not reduced.
5.7 Lemma If a CODG is
sp-consistent, is reduced, and has a single root, then it is isomorphic to a
noDAG; thus, by M2008, it is oo-serializable iff it is
completion-acyclic.
5.8 Definition Let G be a CODG. A
single-rooted extension (sre) of a G, is
identical to G with an added root that has as children the roots of the
original CODG, in some ordering, without
repetition.
Note that, in general, a CODG has more than one sre (in effect, n!,
where n is the number of roots in the original CODG, i.e., one for each
possible ordering of the original roots).
5.9 Lemma A CODG is oo-serializable
iff it has an sre that is oo-serializable.
Proof sketch. (←): Let G be a
CODG, and H an oo-serializable sre of G. Let D be any serialization of H.
Because H has only one root, and D corresponds to H, there must be a range in D
that contains all the others. Thus, the first and last tag of H must be
matching tags. By “removing” those tags from D, we obtain an
oo-serialization of G.
(→): Let G be an oo-serializable CODG, and D any serialization
of G. By “adding” a start-tag and a matching end- tag at
(respectively) the beginning and end of D, we obtain a document that can be
shown to correspond to some sre of G.
We are now ready to state our first main result:
5.10 Theorem There exist CODGs that
are completion-acyclic but not oo-serializable.
Proof sketch. The theorem follows
from the observations that:
-
Each of Examples 2.2 and 6 is completion-acyclic.
-
Each of Examples 2.2 and 6 has exactly two sres, each of which is
sp-consistent, reduced, and (by definition of sre) has a single root.
-
Each sre of each of Examples 2.2 and 6 is completion-cyclic.
By Lemma 5.7, none of Examples 2.2 and 6 has an sre that is
oo-serializable. Thus, by Lemma 5.9, none of Examples 2.2 and 6 is
oo-serializable.
Our second main result is easiest seen as a corollary to the proof of
the preceding theorem. First, we define:
5.11 Definition A CODG is said to be
fully-completion-acyclic (FCA) iff it has an sre
that is completion-acyclic.
5.12 Theorem A CODG is
oo-serializable iff it is fully-completion-acyclic.
Proof sketch. The theorem follows
from the proof of the preceding theorem and the following lemma:
5.13 Lemma If a CODG is not
sp-consistent or is not reduced, then it is not completion-acyclic.
6. Checking full-completion-acyclicity
An obvious way to check whether a CODG is fully-completion-acyclic is to try
out all possible sres and see if at least one is completion-acyclic. From a
completion-acyclic sre, it would be easy to derive an oo-serialization
of the CODG. However, since there are n! different sres to check (where n is
the number of roots in the CODG), this can be very inefficient. It would be
nice to be able to check whether a CODG is fully-completion-acyclic without
having to generate all possible sres.
It turns out it suffices to check each pair of roots for a particular
condition which is verifiable in polynomial time. Since there are n × (n - 1)
/ 2 root-pairs and checking the condition can be done in polynomial time, it
follows that full-completion-acyclicity can in fact be checked in polynomial
time.
The condition to be checked is as follows.
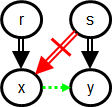
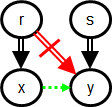
6.1 Definition Let r and s be two roots of
some CODG G = (V, ch) that are unordered with respect to ssb(G). We say that r
must precede s, noted r ↝ s, iff there
exist vertices x and y standing in either (or both) of the following configurations
with
respect to r and s:
Here, the double-arrows represent the reachability (⇒) relation, not just
parent-child relationships. The red double-arrow (with a stroke through it)
means the complement of ⇒ (thus, in Configuration 1, s ⇏ x). It does not
matter whether or not r ⇒ y (resp. s ⇒ x) in Configuration 1 (resp.
Configuration 2). In other words, at least one of r
⇏ y and s ⇏ x must be the case. The dotted green arrow means that (x, y) ∈
(ssb − ⇒), in other words, that x precedes y without being an ancestor of
it.
An instance of at least one of those configurations is found in each of the following
CODGs:
6.2 Lemma Let G be a CODG, and r and s be
two roots in G such that r ↝ s. Then, for each H that is a CA sre of G, (r, s)
∈ gsp(H).
Proof sketch. If there exists no CA sre of G, or if
there are no two roots r and s in G such that r ↝ s, then the lemma is
vacuously verified. Let thus H be any CA sre of G and, for the sake of
contradiction, suppose r and s are two G-roots such that r ↝ s and such that
(r, s) ∉ gsp(H). Suppose x and y are two vertices as in Configuration 1
above (we prove only the case of Configuration 1; that of
Configuration 2 is proved similarly).
By the definition of sre, if (r, s) ∉ gsp(H), then it must be the case that
(s, r) ∈ gsp(H), and thus, by construction of ssb(H) (Definition 4.3-2),
that (s, r) ∈ ssb(H). Hence, it follows by Lemma 4 of M2008 and the fact that r and s do not stand in
ancestor-descendant relationship (being both G-roots, they are
⇒-incomparable), that (r, s) ∈ sea(H). Similarly, from (x, y) ∈ ssb(H) and x ⇏
y, and y ⇏ x (because (x, y) ∈ ssb(H)), we conclude that (y, x) ∈
sea(H).
Now, by construction of sea(H) (Definition 4.3-4), and from the facts
that r ⇒ x, that (r, s) ∈ gsp-1(H), and that s ⇏ x,
we conclude that (x, s) ∈ sea(H). So, we have (y, x) ∈ sea(H) (established
earlier), and (x, s) ∈ sea(H), and (s, y) ∈ sea(H) (because s ⇒ y). Thus,
sea(H) is cyclic, contrary to our hypothesis that H is CA, and so we must
reject the hypothesis that (r, s) ∉ gsp(H), and conclude that (r, s) ∈
gsp(H).
QED
6.3 Theorem A CODG is FCA iff it is CA and
it does not have any two roots r and s such that r ↝ s and s ↝ r.
Proof sketch.
(⇒) Any FCA CODG is CA. If a CODG had roots r and s such that r ↝ s and s ↝
r, then by Lemma 6.2, it would have a cycle in ssb, and thus could not be
CA.
(⇐) Let G be a CA CODG in which no two roots r and s are such that r ↝ s and
s ↝ r. Note that by Lemma 5.13 and the fact that G is CA, we know that G
is sp-consistent and reduced, and will thus take this for granted.
We give an algorithm for constructing an ordering of the roots of G that can
be used as the root-order in a sre H of G which will be shown to be FCA. In
the algorithm, ssb(G, ROR) denotes the result of building ssb as per
Definitions 4.3-1 and 4.3-2, but using gsp(G) ∪ ROR instead of
gsp(G)
Algorithm:
-
Let ROR = { (r, s) | r and s are roots in G and r ↝ s }.
-
Let SSB = ssb(G, ROR).
-
WHILE (∃ x, y ∈ V)[ch(x) = ch(y) & {(x, y), (y, x)} ∩ SSB =
∅]
-
Pick any x and y satisfying the WHILE clause, and
let X = x, and Y = y.
-
Let ROR = ROR ∪ {(r, s) | r and s are roots in G,
and r ⇒* X, and s
⇒* Y}.
-
Let SSB = ssb(G, ROR).
When the algorithm stops, ROR is the root-order to be used for
constructing H.
The intuition behind the algorithm is best conveyed with examples.
Essentially, the algorithm goes like this: start with the root-orderings that
are imposed by the topology of the CODG, i.e., those pairs of roots (r, s) for
which r ↝ s. Then, for the other root-pairs, they can basically be ordered
randomly, as long as no silly decision
is taken.
To see what silly decisions
would be, consider
Example 10. A silly decision would be to stick root r between s and t. To
avoid such decisions, the root-ordering must be built gradually, considering
one by one (the order does not matter) the unordered pairs of parents of the
same children. For each such pair (x, y), decide of an arbitrary order, then,
make sure all roots reachable upwards from x come before all those reachable
upwards from y (there can be no root reachable both ways, otherwise, x and y
would have been ordered to start with).
Each time such root-orderings are added, the consequences on the global ordering
of the CODG are recomputed and propagated down from the roots.
Example 11 provides a more intricate example, in which eight possible
pairs of unordered parents of the same children exist: (u, w), (u, x), (v, w),
and (v, x), and their inverse. Whichever pair is chosen, it will result in roots r
and s
being ordered at step 3b, and then, in all eight pairs being ordered at
step 3c.
Examples 12 and 13 show that the addition of a leaf can cause some
root-pairs to be ordered from the start: (r ↝ s) and (r ↝ t) in
Example 12; (r ↝ s) in Example 13.
Proof sketch of termination: At each turn, at least one
pair of the kind sought for in (3) is ordered. Indeed, it can be shown that
the chosen pair (x, y) causes arcs to be added to ROR that will necessarily
order the pair (x, y) itself. Thus, eventually, no pair satisfying the WHILE
clause will remain.
Proof sketch that ROR orders all pairs of roots: The
existence of an unordered root-pair
implies that there is a pair satisfying the WHILE clause. Thus, when no more
such pair exists, all the roots
have been ordered.
Proof sketch that ssb(G, ROR) is acyclic: Any condition
that might cause a cycle would also cause a cycle in { (r, s) | r and s are
roots in G and r ↝ s }, a contradiction.
A rough analysis of the algorithm shows that its running time is polynomial
(probably with degree at most 3 or 4). Obviously, it could be used to actually
build a CA sre of any FCA CODG, and thus an oo-serialization of the CODG. This
establishes a polynomial upper-bound on the task of verifying
full-completion-acyclicity and of generating an oo-serialization of a FCA
CODG. While interesting, we do not believe these upper-bounds to be tight, and
hence consider the exact complexity of these tasks to be open
questions.
7. Conclusion and future work
In this paper, we defined a class of graphs, child-arc-ordered directed graphs (CODGs), that includes
multi-graphs and non-acyclic graphs, and investigated the conditions under
which a CODG is “oo-serializable”, i.e., has a structure which
corresponds to that of an overlap-only marked-up document. We found that the
property of completion-acyclicity does not
guarantee oo-serializability in general for CODGs, by showing that there exist
completion-acyclic CODGs that are not oo-serializable. By contrast, Marcoux
has shown that for the less general class of node-ordered-DAGs (noDAGs), completion-acyclicity does
guarantee oo-serializability M2008.
We then defined a condition strictly stronger than
completion-acyclicity, full-completion-acyclicity, and showed that it does
guarantee oo-serializability for all CODGs.
Finally, we presented polynomial-time algorithms for checking
full-completion-acyclicity and for computing an oo-serialization of
fully-completion-acyclic CODGs. However, we do not believe these algorithms to
be optimal. Thus, open questions include determining the exact complexity of
— and finding optimal algorithms for — checking
completion-acyclicity, full-completion-acyclicity, and of actually computing
an oo-serialization of a CODG once it is found to be serializable.
Another area of research we hope to pursue in the near future is
investigating whether and how some forms of interrupted and virtual elements,
as found in TexMecs, can be characterized in terms of graphs.
Appendix A. Notation and symbols
For the convenience of readers who find the notation used
here unfamiliar, we list here the symbols and conventional
variable names used in this paper.
|
↝
|
the must-precede relation on roots of a graph
G: r ↝ s if and only if there exist vertices x and y standing in some
specific configurations with respect to r and s (see Definition 6.1).
|
|
⇒G
|
the positive transitive closure of
E(G), for any graph G; sometimes known as the
reachability relation of G; often abbreviated
to ⇒ when the identity of G is understood.
|
|
⇒*G
|
the reflexive transitive closure of
E(G), for any graph G; often abbreviated
to ⇒* when
the identity of G is understood.
|
|
∈
|
is an element of. So x ∈
y means that x is an element in the
set y.
|
|
∪
|
set union. So x ∪ y
denotes the set of all elements which are members either
of set x or of set y or both.
|
|
∩
|
set intersection. So x ∩ y
denotes the set of all elements which are members of
both set x and set y.
|
|
ap(G)
|
the ancestral-precedence relation of a graph G;
abbreviated ap when G is understood. This is a binary
relation consisting of all node pairs (v, w) for which
(informally) v is an ancestor of w and not vice-versa.
|
|
ch
|
(core meaning) a unary function that maps each
node of a graph to a sequence of nodes of that
graph.
(secondary meaning) a two-argument function that
maps from a pair (v, n) (where v is a node and n is
an integer) to at most one node among the children of v.
|
|
ch(v)
|
for any node v in a graph G,
ch(v) denotes a sequence of nodes in
G.
Note that sequences are typically modeled as
sets of pairs (n, e) where n is a number and e an
element of the sequence. The set of pairs
denoted by ch(v) can thus be treated as a function
from non-negative integers to nodes in the graph:
for any node v and any suitable integer
n, ch(v)(n) denotes the nth child of v;
ch(v)(0) denotes the first child, ch(v)(1) denotes
the second, etc. To reduce the need for parentheses,
ch(v)(n) is normally written in the
simpler form ch(v,n) .
|
|
ch(v, n)
|
denotes the nth child (counting from 0)
of node v. This is a short-hand form for the
expression ch(v)(n).
|
|
E(G)
|
the set of arcs in a graph G
|
|
G
|
the conventional variable for a graph (here
invariably a CODG)
|
|
gsp
|
a shorthand form of gsp(G) when the identity of
the graph G is understood.
|
|
gsp(G)
|
the global sibling-precedence relation of a graph G;
written as sp when G is understood.
This is (speaking informally) a relation consisting of all
node pairs (v, w) which share a parent, and for which v
precedes w among the children of that parent. Note that
the same pair of children may share more than one parent,
occurring in one order for one parent and in the other
order for the other parent. So gsp(Example 2.3)
includes both (b, c) and (c, b).
|
|
N
|
the natural numbers (0, 1, 2, ...)
|
|
n, m
|
conventional variables used to represent
individual natural numbers
|
|
r
|
conventional variable used to denote an
arbitrary range.
|
|
r1
|
for a given range r,
r1 denotes the first
element of r.
|
|
r2
|
for a given range r,
r2 denotes the second
element of r.
|
|
r, s
|
conventional variables used to denote two
roots of a CODG.
|
|
sea(G)
|
the should-end-after relation
of a graph G; abbreviated sea when G is
understood
|
|
seaa(G)
|
the should-end-after additions
relation of a graph G; abbreviated seaa
when G is understood
|
|
sp
|
a shorthand form of sp(G) when the identity of
the graph G is understood.
|
|
sp(G)
|
the sibling-precedence relation of a graph G; this is
a ternary relation consisting of all node triples (v, w,
x) for which (informally) w precedes x among the children
of v; note that if w occurs more than once among the
children of v, then the triple (v, w, w) appears in
sp. If some node x occurs between the two occurrences of
w, then (v, w, x) and (v, x, w) are both in sp.
|
|
sre
|
single-rooted extension of some graph G. Note that
any multi-rooted graph G has many single-rooted extensions
(one for each possible ordering of the roots of G).
|
|
ssb(G)
|
the should-start-before
relation of a graph G; abbreviated ssb when
G is understood
|
|
ssba(G)
|
the should-start-before
additions relation of a graph G; abbreviated
ssba when G is understood
|
|
V
|
the set of nodes (or vertices) in a graph;
a short-hand for V(G)
|
|
V(G)
|
the set of vertices in a graph G
|
|
V × V
|
the Cartesian product of V, the set of nodes;
that is, the set of pairs (v, w) where v ∈ V and w
∈ V
|
|
V × V × V
|
the set of triples (v, w, x) where v, w and x
are all ∈ V.
|
|
v, w, x, u
|
variables conventionally used
for individual nodes in a graph (by convention, all of
v, w, x, u ∈ V)
|
References
[B1995] David Barnard, Lou Burnard, Jean-Pierre
Gaspart, Lynne A. Price, C. M. Sperberg-McQueen, and Giovanni Battista Varile.
“Hierarchical Encoding of Text: Technical Problems and SGML
Solutions”, in Computers and the
Humanities, 29/3 1995, pp. 211-231.
http://www.springerlink.com/content/p7775247276v88h3/, http://xml.coverpages.org/barnardHier-ps.gz. doi:https://doi.org/10.1007/BF01830617
[D2004] Steven DeRose. “Markup Overlap: A
Review and a Horse”. Paper delivered at Extreme Markup
Languages, 2004, Montréal.
http://conferences.idealliance.org/extreme/html/2004/DeRose01/EML2004DeRose01.html
[HS2003] Claus Huitfeldt and C. M. Sperberg-McQueen.
TexMECS: An experimental markup meta-language for complex
documents. University of Bergen, January 2001, rev. October 2003.
http://mlcd.blackmesatech.com/mlcd/2003/Papers/texmecs.html
[M2008] Yves Marcoux. Graph
characterization of overlap-only TexMECS and other overlapping markup
formalisms. Proceedings of the Balisage
2008 conference, 12-15 august 2008, Montréal (Canada).
doi:https://doi.org/10.4242/BalisageVol1.Marcoux01
[M2012] Moore, Neil. Multihierarchical documents
and fine-grained access control (2012). Theses and
Dissertations--Computer Science. Paper 6. http://uknowledge.uky.edu/cs_etds/6
[SH2004] C. M. Sperberg-McQueen and Claus Huitfeldt.
GODDAG: A Data Structure for Overlapping
Hierarchies. Springer-Verlag (2004).
Preprint at
http://cmsmcq.com/2000/poddp2000.html
[SH1999] C. M. Sperberg-McQueen and Claus Huitfeldt:
“Concurrent Document Hierarchies in MECS and SGML”, in
Literary and Linguistic Computing, 14 1999,
pp. 29-42.
http://llc.oxfordjournals.org/cgi/content/abstract/14/1/29. doi:https://doi.org/10.1093/llc/14.1.29
[W2005] Andreas Witt. “Multiple Hierarchies: New
Aspects of an Old Solution”, in: Stefanie Dipper, Michael Götze, and
Manfred Stede (eds.), Heterogeneity in Focus: Creating
and Using Linguistic Databases, vol. 2 of Interdisciplinary
Studies on Information Structure (ISIS), Working Papers of the SFB 632.
University of Potsdam, Germany, 2005. (Corrected reprint of an Extreme Markup
2004 paper.)
http://www.sfb632.uni-potsdam.de/publications/isis02_4witt.pdf
×Yves Marcoux. Graph
characterization of overlap-only TexMECS and other overlapping markup
formalisms. Proceedings of the Balisage
2008 conference, 12-15 august 2008, Montréal (Canada).
doi:https://doi.org/10.4242/BalisageVol1.Marcoux01
×Andreas Witt. “Multiple Hierarchies: New
Aspects of an Old Solution”, in: Stefanie Dipper, Michael Götze, and
Manfred Stede (eds.), Heterogeneity in Focus: Creating
and Using Linguistic Databases, vol. 2 of Interdisciplinary
Studies on Information Structure (ISIS), Working Papers of the SFB 632.
University of Potsdam, Germany, 2005. (Corrected reprint of an Extreme Markup
2004 paper.)
http://www.sfb632.uni-potsdam.de/publications/isis02_4witt.pdf