Introduction

We propose to extend the familiar type/token distinction in two ways. First, we apply it not only to words or to atomic characters but also to higher-level document structures; second, we introduce mechanisms for handling tokens whose type identity is ambiguous either because of uncertainty or because of intentional use of multiple meanings. In the first point, we follow the example of a number of other authors who have distinguished at multiple levels what we here call tokens from what we here call types; we offer a more explicit and formal account than has been usual. Recasting the familiar type/instance distinction as a type/token distinction has the helpful consequence of providing a unified account of document structure at all levels, instead of treating the character and element levels as essentially different.

The ideas presented here originally arose (as some of the examples will show) in the context of work on the logical structure of transcription, but they concern general questions of document structure.

The next section (section “The type/token distinction”) presents a terse survey of the type/token distinction, as we believe it is conventionally accepted. The following section (section “Extensions to the conventional view of types and tokens”) elaborates the conventional view and extends it in three ways. First, our account handles not only atomic but also compound types; our compound types and compound tokens include the structures conventionally recognized and marked up in descriptive markup. Second, we propose a mechanism that handles not only the usual case in which a token has a single known type, but also less common and more difficult cases in which there is uncertainty about which type to assign to a token, or in which a token has been intentionally designed to belong to multiple types. Third, we introduce the notions of type repertoire and type system to clarify the ways in which multi-level types and tokens obey the normal rule stipulating that any token instantiates just one type. The penultimate section (section “Types, tokens, and markup languages”) discusses some of the obvious parallels between markup languages like XML and the application of the type/token distinction to document structures at levels above the individual character or word. The final section (section “Conclusion”) contains some concluding remarks and speculations.

The type/token distinction

The distinction between strings as types and strings as tokens is a familiar one to almost any programmer, but what they have in mind is not quite the same as was described by Peirce when he introduced the distinction [Peirce 1906].

Consider a sequence of words on a page, for example the first sentence of the Algol 60 report [Naur et al. 1960], and the question How many words are in this sentence?

After the publication of a preliminary report on the algorithmic language ALGOL, as prepared at a conference in Zürich in 1958, much interest in the ALGOL language developed.

In one sense, there are 28 words; the sentence is a sequence of words, and the length of the sequence is 28. In another sense, however, the sentence contains only 21 words (assuming that 1958 counts as a word), some of which (ALGOL, a, in, language, and the) appear more than once. In some contexts, it would be convenient to treat these repeated words as distinct, and in other contexts, to treat them as identical.

Peirce provided a simple way to do this, by distinguishing the two senses of word at issue here. He called words in the first sense tokens and in the second sense types. A token, in Peirce's account, is a thing which is in some single place at any one instant of time — this example, the tokens are the physical marks of ink on the page (or the physical illumination of the pixels on the screen). Types, meanwhile, are in the usual account the abstract objects we identify when we say that the second and ninth words (tokens) of the sentence are the same word.

Peirce's account

Peirce's account of the distinction runs as follows [Peirce 1906] pp. 423-4:

A common mode of estimating the amount of matter in a MS. or printed book is to count the number of words. There will ordinarily be about twenty thes on a page, and of course they count as twenty words. In another sense of the word word, however, there is but one word the in the English language; and it is impossible that this word should lie visibly on a page or be heard in any voice, for the reason that it is not a Single thing or Single event. It does not exist; it only determines things that do exist. Such a definitely significant Form, I propose to term a Type. A Single event which happens once and whose identity is limited to that one happening or a Single object or thing which is in some single place at any one instant of time, such event or thing being significant only as occurring just when and where it does, such as this or that word on a single line of a single page of a single copy of a book, I will venture to call a Token. [...] In order that a Type may be used, it has to be embodied in a Token which shall be a sign of the Type, and thereby of the object the Type signifies. I propose to call such a Token of a Type an Instance of the Type. Thus, there may be twenty Instances of the type the on a page.

As may be seen, Peirce's distinction stresses the opposition between the concrete physical existence of the token and the abstract nature (and, in Peirce's terminology, the non-existence!) of the type. He also establishes the usage that tokens can be said to instantiate types.[1] To be a token, in fact, is to instantiate a type (and vice versa); there are no tokens without associated types.[2]

Other usages of type and token

There are a number of other usages of the terms type and token which differ from Peirce's, and should not be confused with it.

Peirce's types have nothing to do with Bertrand Russell's logical types, which are classes or orders of sets and belong to a completely different story. The (data) types of programming languages and XML schema languages are similarly distinct concepts.

Some common usages (not only in computing, but particularly visible there), employ an opposition between token and type similar to Peirce's, but divorce it more or less completely from the opposition of concrete physical existence and abstraction; any instance of a particular string (more precisely, of a particular string type) is taken as a token of that type. In a related usage, token is also taken simply as one item in the results produced by a tokenizer, whose task it is to divide a sequence of characters into units. A more careful usage reserves the word token for concrete physical phenomena and uses the term occurrence for what common computing terminology calls tokens, reserving token for particular physical realizations of the type.[3]

In this paper, we do distinguish between tokens, types, and occurrences of types. The latter will be encountered mainly in what we will call compound types, for example sets or sequences of (other) types. In those cases, the components of the compound type are implicitly understood to be occurrences of types, so we will not say, for example, sequence of occurrences of types (which would be somewhat pleonastic), but simply sequence of types.

Related distinctions

The type/token distinction is sometimes met with under different names (and those who use those different ways of speaking about things may or may not agree with our claim that what they are speaking about is in fact the type/token distinction). In this section we mention two of the more important, without being able to discuss them in the detail they deserve.

Nelson Goodman describes the constituents of a notational system thus [Goodman 1976], p. 131:

Characters are certain classes of utterances or inscriptions or marks. (… an inscription is any mark — visual, auditory, etc. — that belongs to a character.) Now the essential feature of a character in a notation is that its members may be freely exchanged for one another without any syntactical effect; or more literally, since actual marks are seldom moved about and exchanged, that all inscriptions of a given character be syntactically equivalent. In other words, being instances of one character in a notation must constitute a sufficient condition for marks being true copies or replicas of each other, or being spelled the same way.

Goodman speaks here of characters being classes of inscriptions, but he makes clear elsewhere that this is merely a convenient way of expressing himself and is not intended to commit him to the existence of classes or sets: in a more careful formulation, presumably, Goodman would say that characters are the mereological sums of their inscriptions: complex individuals (entities) made of the individual inscriptions of the character.[4]

We take Goodman's opposition between inscription and character to be the same as, or very similar to, Peirce's opposition of token and type. The properties Goodman ascribes to characters and inscriptions are precisely those of types and tokens. Goodman makes explicit some properties of types and tokens which are part of the usual view of the matter but are not explicit in the passage from Peirce quoted above. In particular:

  • No token is a token of more than one type.[5] In consequence, types are disjoint from each other.

  • Any two types must be finitely differentiated from each other; it must always be possible, in principle, to distinguish tokens of one type from tokens of another. (This does not mean that it will always be easy or possible in practice, only that in any system of types it is not possible to have two which are not in principle distinguishable from each other.)

The full exploitation of Goodman's work for illumination of the type/token distinction remains a desideratum for the future.

The type/token distinction also resembles the distinction made by most phonologists between specific individual sounds or configurations of the vocal organs (phones) and the distinctive units of phonology (phonemes).[6] Goodman's remark about the equivalence (at least for syntactic purposes) of the different tokens of a type recalls the occasional supposition by phonologists that different realizations of the same phoneme may be interchanged freely without affecting the acceptability of the utterance.

The phone/phoneme distinction allows linguists to treat sounds in different utterances (or at different locations in the same utterance) as identical for certain purposes, and distinct for others. It thus serves a function analogous to the one we noted above for the type/token distinction. Like types, phonemes are instantiated by physical phenomena which can vary widely in detail. Like types, they are taken to be disjoint from each other (they serve, in a common description, as contrastive units, which we take to mean that one of their functions is to be distinct from each other).

Much of the machinery of phonology can usefully be applied to types and tokens. Just as phonemes can almost always be realized by a number of different phonetic variants (allophones), with the choice of allophone often determined by the phonetic environment, so also do the tokens of a type frequently fall into subclasses which may vary depending on environment or other factors. Conventionally minimal pairs (pairs of words which differ only in a single sound) are taken as evidence for distinctions among phonemes; similarly minimal pairs can be used to distinguish different types from each other. And just as phonologists have found it helpful to define phonemes in terms of sets of minimally distinctive features, so also it may prove helpful to define types in terms of distinctive features. It is interesting to note that defining types in terms of finite sets of distinctive features guarantees that any type so defined will satisfy Goodman's requirement that it be finitely differentiated from other types.

Types and tokens at different levels

One further topic should be discussed at least briefly before we proceed with our elaboration of the type/token distinction. As the title of the paper indicates, its central idea is that the type/token distinction can be applied not just to words and characters, but also to higher-level document structures. Since document structures are generally understood to have internal structure and to nest within other document structures, we must necessarily consider both types and tokens as capable of nesting and having internal structure.

This appears not to be the most common view of the type/token distinction. The distinction is sometimes applied at the character level, and sometimes at the type level, but not (usually) at both levels at the same time. In the passage quoted above, for example, Peirce identifies types and tokens only as ways of looking at words, without mentioning their relation to types or tokens at lower or higher levels of analysis.

It is not unknown, however, to apply the type/token distinction at multiple levels.

Goodman, for example, explicitly applies the term character things which may contain other characters, and expects this to be the normal case: Any symbol scheme consists of characters, usually with modes of combining them to form others. So in Goodman's sense, the initial A of ALGOL is a character, and so is ALGOL itself. The first sentence of the Algol report can be regarded as a character in the same sense, as can the paragraph in which it occurs, and after a few more combinations at higher and higher levels, the Algol 60 report itself as a whole. (Or, in the terminology we prefer as less confusing to users of Unicode, the initial A of ALGOL, the word ALGOL itself, and so on, are all types at various levels, instantiated by tokens at similarly various levels.)

The linguistic concept of phone and phoneme does not allow phonemes to nest. But the idea of phonetic/phonemic contrasts has been widely applied in other areas of linguistics, perhaps most widely and visibly by the linguist Kenneth L. Pike. Pike generalized the distinction between phonetic and phonemic phenomena, coining the terms emic and etic, and applied the distinction not only to other areas of linguistic analysis but also to virtually all of human behavior [Pike 1967]. The emic/etic distinction has apparently achieved wide currency in some schools of anthropology and sociology. And when both phonological and other linguistic levels are analysed in terms of emic and etic units, it is unavoidable that some of those units will have internal structure and nest in other emic and etic units.

Finally, recent discussions of types and tokens by the philosopher Linda Wetzel have devoted significant attention to questions that arise when considering tokens, or types, at multiple levels. If we consider any concrete realization of the sentence from the Algol report quoted above (i.e. any token of the sentence), then it is easy enough to see that the sentence token can be decomposed into word tokens, and the word tokens into character tokens. But of what, asks Wetzel, is the sentence type composed? It cannot be composed of word tokens, because as a type it is abstract. It cannot be composed simply of word types, because the sentence is 28 words long, but there are only 21 word types available for the job. Wetzel concludes, after painstaking investigation of alternatives, arguments, and counter-arguments, that the sentence type consists of 28 occurrences of word types. She elucidates the concept of occurrence with the aid of an appeal to sequences, and then generalizes it to situations where the parts of a larger whole are not arranged in sequences.

Another issue raised by Wetzel may be worth mentioning. In cases where the containing string is written out in full, each token in the string will (as always) constitute a different occurrence of a type, and each occurrence of a type will be signaled by a different token. This has led some philosophers to doubt the utility of any distinction between occurrences and tokens. How, they ask, can a type occur multiple times in a sequence (or other structure) unless it is instantiated by a different token for each occurrence? The question takes on a particular interest in the context of SGML and XML, where multiple references to an entity can in fact easily produce multiple occurrences of a type from a single token. Macros as handled by the C pre-processor have the same effect. Examples outside of mechanical systems appear to be less common, but they do exist. In printed versions of ballads and other songs with refrains, it is not uncommon for only the first occurrence of the refrain to be printed in full, while others are indicated only by the word Refrain, which functions here as a sort of macro or entity reference. And repeat-marks in music seem to make the note tokens so marked correspond to multiple note-type occurrences in the music.

Extensions to the conventional view of types and tokens

In this section we elaborate and extend the conventional type/token distinction, and provide a formal model for it. The formal model is expressed using the syntax of Alloy, a modeling tool developed by Daniel Jackson and his research team [Jackson 2006].[7] Readers uninterested in formalization may skip the Alloy extracts without loss of context.

Our model goes beyond the most common version of the type/token distinction in three ways:

  1. We follow Goodman, Pike, Wetzel, and others in assuming types and tokens on multiple levels.

  2. We introduce disjunction of types to cover cases in which a reader is uncertain which type is instantiated by a given token, and conjunction of types to cover cases in which a token, contrary to the usual rule, instantiates multiple types.

  3. We introduce explicit notions of type repertoires and type systems as a way of resolving the contradictions that otherwise arise from assuming both (a) that several levels of type and token can coexist, and (b) that, as already noted, types are necessarily disjoint.

Basic concepts

The basic concepts of the model we propose can be summarized as follows.

The key concepts of the model are those of token and of type, which are defined partly in opposition to each other.

  1. Tokens are concrete physical phenomena: marks on paper, magnetic pulses on disk or tape, etc.

But not all physical marks are tokens: a mark is recognized as a token if and only if it is recognized as being a token of some type.[8] The recognition of tokens as instances of particular types requires a competent observer (e.g., a human reader, in the case of conventional writing), but we do not here address the perceptual and psychological processes by which humans recognize a token as being of a particular type.

  1. Types may be regarded as abstract objects represented or symbolized by tokens.

Alternatively (in the spirit of Goodman's calculus of individuals) they may be regarded as collective individuals whose constituent parts are tokens.[9]

In either case, we will say that tokens instantiate types, and that types are normally conveyed or communicated by being instantiated by tokens.

  1. Each token instantiates exactly one type.

It must instantiate at least one type, because a mark that does not instantiate a type is not a token. And it cannot instantiate more than one type, because types are mutually disjoint and no token can be of multiple types. (At least, this is the simplest way to start out. But see further the discussion of type repertoires and type systems below.)

In more formal terms: types have identity, but we specify no other properties for them. 

abstract sig Type {}

Tokens map to types. The only salient property of a token, and thus the only property we model, is the identity of the type it instantiates.[10]

abstract sig Token {
 type : Type
}

The declaration type : Type indicates that the type relation links each Token to exactly one Type. It follows, then, that:

  • Each token instantiates exactly one type.

  • Any two types are instantiated by disjoint sets of tokens.

Multiple levels of types and tokens

As noted above, earlier authors have contemplated types and tokens which have internal structure and nest; here we take up that principle and formalize it.

  1. Some tokens are basic, or atomic in the sense that no other tokens are part of them; the types instantiated by them are similarly basic.

Simple examples are the characters of the Latin alphabet and punctuation marks.

Formally: basic types are a kind of type, and basic tokens are a kind of token. The types to which basic tokens map will normally be basic types, but for reasons clarified below this is not required by the model. 

sig Basic_Type extends Type {}
sig Basic_Token extends Token {}

  1. Other tokens are compound: aggregations or collections of lower-level tokens; so also with types.

We refer to the lower-level types or tokens as the constituents of the higher-level one of which they form a part.

Because in written documents compound tokens typically occupy a discernible and possibly large region of the text carrier, we call them regions. Because compound types are, in the usual case, structural units of a kind familiar to any user of SGML or XML for document markup, we refer to them as S_Units.

Regions can be decomposed into subregions and S_Units have children. It proves useful to postulate that S_Units also have a set of property-value pairs, and are labeled as to their type or (to avoid overloading the word type yet again) their kind.

Formally: compound types and tokens are subsets, respectively, of types and tokens generally. They have subordinate types and tokens, referred to as their children and subregions, respectively. 

abstract sig Region extends Token {
  subregions : set Token
}{ 
  type in S_Unit
  type.children = subregions.@type
}
abstract sig S_Unit extends Type {
  kind : lone Kind,
  props : set AVPair,
  children : set Type
}

  1. The lower-level items in compounds are frequently arranged in a sequence, but this is not invariably so. The constituents (subregions and children) may also form a set, or a bag.

Simple examples of sequence include the aggregation of sequences of character tokens to form word tokens and similarly the aggregation of sequences of character types to form word types. At higher levels, the aggregation of paragraphs to form a chapter, or of chapters to form a novel, provide further examples. Sets and bags are less frequent in documentary applications, but not unknown; they occur whenever it is meaningless or misleading to ask about the order of the children, or when the children are represented in some sequence of tokens which is explicitly stated to carry no significance.

Formally: 

sig Ordered_Region extends Region {
 sub_seq : seq Token
}{
  elems[sub_seq] = subregions
  type in Ordered_S_Unit
  type.ch_seq = sub_seq.@type
}
sig Ordered_S_Unit extends S_Unit {
  ch_seq : seq Type
}{
  elems[ch_seq] = children
}

The declaration sub_seq : seq Token says that each Ordered_Region is associated with a sequence of (sub)tokens; ch_seq : seq Type says the analogous thing for Ordered_S_Unites. The declarations elems[sub_seq] = subregions and elems[ch_seq] = children specify that the elements of those sequence are precisely the constituents of the compound object. The declaration type in Ordered_S_Unit requires that any ordered region instantiate an ordered type.[11] The declaration type.ch_seq = sub_seq.@type specifies that for any ordered region R, the children of R's type are the types of R's subregions.

Next, we turn to unordered types and tokens (bags and sets): 

abstract sig Unordered_Region extends Region {}{
  type in Unordered_S_Unit
}
abstract sig Unordered_S_Unit extends S_Unit {}

Note that those definitions make Ordered_S_Unit and Unordered_S_Unit disjoint from each other, as expected (an S_Unit cannot be both ordered and unordered).

Types and tokens whose constituents are unordered have either set structure or bag structure. Set-structured tokens map to set-structured types (and ditto for those with bag structure). Bag-structured types and tokens keep track of the number of occurrences of each constituent (modeled here by the functions sub_counts and ch_counts, which map from constituents to natural numbers. 

abstract sig Set_Structured_Region extends Unordered_Region {}{
  type in Set_Structured_S_Unit
}
abstract sig Set_Structured_S_Unit extends Unordered_S_Unit {}

abstract sig Bag_Structured_Region extends Unordered_Region {
  sub_counts : subregions -> Natural_number
}{
  type in Bag_Structured_S_Unit
}
abstract sig Bag_Structured_S_Unit extends Unordered_S_Unit {
  ch_counts : children -> Natural_number
}

Normally, basic tokens instantiate basic types; exceptions are the disjunctive and conjunctive types defined below. Only compound tokens can successfully instantiate most compound types, because of the rule type.children = subregions.@type in the declaration of regions. Essentially, this requires a kind of compositionality: if the type of a region has child types, then those child types must be instantiated by subregions of the region. Since basic tokens have no subregions, they cannot satisfy this constraint.

Several observations can be made about compound types and tokens.

The lowest level of compound, consisting of a sequence of basic tokens (or types), is frequently an object of special interest. (For example, the text node of the XPath data model is characterized precisely by being a sequence of Unicode characters [here taken as basic] uninterrupted by markup and without any further properties or structure.)[12]

Basic tokens consist of marks on a text-bearing writing medium; compound tokens consist of collections of other tokens (basic or compound); not infrequently, these are physically proximate and so compound tokens may be identified with regions of the text carrier.[13]

The compound types instantiated by compound tokens are not infrequently structural units of the kind identified by elements and attributes in standard markup practice.

Among the compound tokens, the document itself is an important edge case, and similarly the text among compound types.[14]

Finally, some ancillary declarations are needed for the Kind, AVPair, and Natural_number objects appealed to in some of the earlier declarations.

The signatures Kind and AVPair serve purposes analogous to the generic identifiers and attribute-value pairs of SGML and related markup languages. We do not analyse them further. Natural_number is just an integer greater than zero. 

abstract sig Kind {}

sig AVPair {
  att_name : Kind,
  att_value : Type
}

sig Natural_number {
  theNumber : Int
}{
  theNumber > 0
}

Ambiguity: disjunction, and conjunction

Our model of the type/token distinction goes beyond the conventional view in a second way: we postulate disjunctive and conjunctive types, to address some cases which are otherwise difficult to handle.

In some documents it may be difficult to say just what type is instantiated by some tokens (e.g., if the document is difficult to read). For example, consider the following extract from a manuscript of Ludwig Wittgenstein:

Figure 1

A word in Wittgenstein's 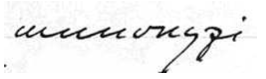Geheimschrift (Item 118, page 8v).

Transcribers not yet aware that this word is written in Wittgenstein's so-called secret writing (in which A is substituted for Z, B for Y, etc., and vice versa) might have difficulty deciphering the token. Transcriber A might render the word as munonyqi, transcriber B as wunouyqi. Both might accept the other's transcription as just as likely as their own. How, in this case, should a neutral observer whose knowledge of the original is derived only from the transcription, or a transcriber uncertain how to read the philosopher's handwriting, characterize the first letter of this word? Is it a w or an m?

We could of course simply insist that each token be mapped to a unique type as a matter of principle, thus forcing a choice among the possibilities: m or w. But it might provide a more accurate depiction of the state of affairs if we specified not that the first letter is an m, or that it is a w, but specified instead that it is either the one or the other.[15]

So we extend the model given above by adding the possibility of disjunctive types.

  1. Some compound types represent a disjunction among their constituents.

In Alloy notation: 

sig Disjunctive_Type extends S_Unit {}{
  kind = Disjunction
  some children
}
one sig Disjunction extends Kind {}
Here again, note that Disjunctive_Type is disjoint from both Ordered_S_Unit and Unordered_S_Unit.

Note that the mapping from token to type remains a function: each token continues to map to a single type, but in cases of uncertainty, that single type simply happens to be a disjunction. Formally, this state of affairs could be handled instead by making the token/type mapping a relation, through which any given token would map to one or more types; we choose to reify the notion of disjunction for reasons which should become clear shortly.

Uncertainty is not the only reason one might wish to map a given token to more than one type. Just as ambiguity in utterance may be either unintentional or intentional, so also polyvalence in the token/type mapping may reflect either the uncertainty of the reader or the purposeful choice of the creator. Some of the most entertaining instances of this phenomenon are the mixtures of calligraphy and puzzle creation known as ambigrams or inversions, in which the marks of a document are carefully constructed to instantiate not single types but two or even more. In the following example, the marks can be read either clockwise or counter-clockwise as tokens of the word infinity.[16]

Figure 2

An inversion. © Scott Kim, scottkim.com. Reproduced by permission.

We extend the model, therefore, to include conjunctive types.

  1. Some compound types represent the conjunction of their constituents: tokens instantiating such types instantiate, at the same time, each constituent of the type.

In Alloy: 

sig Conjunctive_Type extends S_Unit {}{
  kind = Conjunction
  some children
}
one sig Conjunction extends Kind {}

As with disjunctive types, no additional fields or machinery are needed: it suffices to classify a type as disjunctive or conjunctive to make clear how the constituent types relate to each other and to the tokens of the type.[17]

Other cases of willed polyvalence include acrostics (in which individual basic tokens form parts of two compound tokens, not just one) and some simple forms of coded communication (e.g., documents where the intended recipient must read every other word, or every other line, to glean the secret message). These deviate from the normal case in which each token (except the top-most, namely the document) is a constituent of just one higher-level token (and similarly, with appropriate adjustments, for types). In the normal case, that is, both tokens and the types they instantiate can typically be arranged in a simple hierarchy. Violations of this hierarchical assumption do not require a special kind of type like a disjunction or a conjunction; it suffices to avoid requiring that no two tokens, and not two types, share any constituents.

It is not hard to imagine (though it is beyond our ability to provide plausible examples of) cases in which the marks of a document are clearly intended to be polyvalent and thus appear to require a mapping to some conjunctive type, but in which it is not clear which conjunctive type is called for. In such situations, the tokens in question may be regarded as instantiating a disjunctive type whose constituents are conjunctive types. One might also imagine an inversion in which the identity of one conjoined type is certain but the other is not: that may be described by mapping the token in question to a conjunctive type whose constituents are a normal type (compound or basic) and a disjunctive type.

Type repertoires and type systems

It is a fundamental property of types as commonly defined, that types are mutually exclusive: each token instantiates a single type. With the exception of special cases involving accidental or willed ambiguity, a given mark is always an a, or a b, or a c, etc., and never more than one. Essentially, types and tokens form a digital rather than an analog system.

But if types can nest within other types, it is easy to find cases where the same token must instantiate multiple types, at different levels. A token I might at one and the same time instantiate several different types:

  • a character (upper-case Latin letter I)

  • a letter (as opposed to a punctuation character or other non-letter character)

  • a word

  • a pronoun

  • a noun phrase

  • a sentence

  • an utterance

This is not a problem for uses of the type/token distinction which work with a single level at a time; it is a more serious difficulty for a model like ours, in which multiple levels are normally present. In such a multi-level system, it is no longer true that all types are disjoint or that each token instanatiates only a single type. On the other hand, the phenomenon arises only because multiple levels of type are present at the same time, in the same view of things. Within a given level (for some suitable definition of that construct) the conventional rule applies: all types are pairwise disjoint.

We postulate that types can be grouped together in type repertoires in such a way that the disjointness rule holds true not absolutely, but for all types in a repertoire. The token I can be both a character and a word, because the character I is a member of one type repertoire, and the word I is a member of a different type repertoire.

In practice, normal readers reading conventional written documents (or listening to normal spoken utterances) apply several type repertoires in parallel, with complex interactions among them.

A non-empty finite collection of type repertoires we call a type system.

Any particular reading of a document will involve a type system. Different readings of a document may diverge not because of irreconcilable substantive differences, but only because they are applying different type systems. For example, a transcriber of eighteenth-century documents who preserves the distinction between long s and short s, and a transcriber who levels the distinction (perhaps on the grounds that the two forms are in complementary distribution and are thus clearly allographs) do not in fact disagree on what their common exemplar actually says; if they disagree, it is only about the appropriate type system to bring to bear on transcriptions of such material.

In some cases (as in the case of long and short s), the relation between type repertoires is a straightforward refinement/abstraction relation: one repertoire makes finer distinctions than the other and contains more information. In other cases, the relation will be more complex.

Types, tokens, and markup languages

There are noticeable parallels between the structured types and tokens we have described and the analysis of documents underlying many colloquial SGML and XML vocabularies. In both cases, we identify structured units which may occur as parts of larger structured units. In both cases, the same abstract units may be instantiated by different concrete realizations.

The model we have presented has been kept rather abstract and general; we have not attempted to enforce in it any of the structural regularities of SGML and XML, such as strict nesting and hierarchical structure. In fact, as far as we can tell, the abstract model of types and tokens we have sketched provides a model not only for SGML and XML, but for all the other kinds of document markup with which we are familiar: MECS and Cocoa and TexMecs and various batch-formatting languages (TeX, Script, troff, ..), as well as word-processor formats. That is, we believe the model outlined here provides a sort of greatest common denominator for markup systems.

The first implication of our work for markup languages, then, appears to be: element types are types, in the sense of the type/token distinction. Element instances are tokens, in the sense of type type/token distinction. This holds at least for the most common cases in colloquial markup vocabularies.

Since by default, all children are ordered in XML documents, XML itself provides no mechanism for signaling that children are in fact unordered. Since such a signal is sometimes necessary, it is to be expected that some vocabularies will define such a signal — as in fact some (e.g., the TEI) do.

The second implication of our work is that higher-level textual objects like paragraphs, sections, chapters, and books, are not different in kind from the characters appearing in character data in the document. The fundamental distinction in SGML and XML between markup and content appears, on this account, to be a technological artifact which masks the underlying reality that characters, paragraphs, sections, and so on are all objects of the same fundamental kind.

It is true that historical writing systems are most complete, consistent, and explicit for the character level, while the realization of higher-level structures like paragraphs, chapters, etc. tends to be more haphazard and inconsistent. But historical writing systems are virtually always incomplete: they do not capture all the relevant linguistic facts, only enough of them to make it possible to convey information. When an existing writing system is applied in new contexts, it may become necessary (and historically this has often been so) to elaborate the writing system so as to make it more explicit. (The development of vowel pointing in Hebrew and Arabic scripts is a case in point.)

This leads us to the third implication of our work: markup languages form nothing other than the extension of conventional writing systems in order to make them more explicit. That is, the paragraph and chapter types which may be marked up by typical vocabularies for descriptive markup are neither more nor less part of the text than the character data which makes up their content. It is sometimes convenient to regard all markup as a kind of annotation, different in nature from the recording of the text itself. But if our model of types and tokens is correct, then there is no difference in essential nature between the A of the word ALGOL, and the paragraph within which it appears. Both are realized in a document by physical phenomena which are tokens of corresponding types.

For a long time, one of the authors of this paper introduced new users to SGML and XML by saying that markup languages are a way to make explicit (part of) our understanding of a text. To the extent that this suggests a separation between the text and our understanding of it and thus encourages the view that markup is a kind of annotation separate from and additional to the text proper, this formulation now seems misleading. Markup languages are a way to make explicit some aspects of the text, as we understand it.

Conclusion

The assertion that all levels of document structure may be regarded as exhibiting a form of the type/token distinction may have a number of implications, some of which appear to require further elaboration and exploration.

If basic and compound tokens and types form a logical continuum rather than entirely separate levels of representation with entirely different rules, then conceptual models which treat documents as consisting of one or more sequences of characters and a set of character ranges would seem to be imposing a radical distinction in methods of representation between the two levels which has no analogue in the phenomena being modeled.

This view may shed a new light on the practice of some XML vocabularies of using empty elements to represent character types not present in (the current version of) the Unicode /ISO 10646 universal character set. Instead of being an ad hoc solution, practically necessary but conceptually awkward, this approach becomes (on the view outlined here) a natural application of the fundamental fact that UCS characters and XML elements are essentially similar: concrete tokens instantiating types of some writing system.

Just as the phonemic units of a language's sound system can be defined in terms of distinctive features, and specific phones are regarded as instantiating particular phonemes whenever they exhibit the requisite pattern of distinctive features, so also it is possible to define the basic types (graphemes) of a writing system in terms of distinctive features. It would be illuminating to extend the analogy further and define distinctive features for the elements and attributes of markup vocabularies.

The realization of phonemes as phones is subject to variation of many kinds: different regional accents may systematically affect the realization of many phonemes in the system, different speakers have different qualities of voice tone, and individual utterances by the same speaker may vary in many ways either systematically or (as far as analysis can tell) randomly. The realization of graphemes is similarly various: different fonts (in printed books and electronic display), different handwriting styles, different hands, different letter formation at different places. And of course the possibility of systematic changes in realization was historically one of the motive forces impelling the development of descriptive markup in the first place. The parallels and possible differences among these phenomena merit consideration at greater length than is possible here.

References

[Cayless 2009] Cayless, Hugh. 2009. Image as markup: Adding semantics to manuscript images. Paper given at Digital Humanities 2009, College Park, Maryland, June 2009.

[Goodman 1976] Goodman, Nelson. 1976. Languages of art: An approach to the theory of symbols. Indianapolis, Cambridge: Hackett, 1976.

[Jackson 2006] Jackson, Daniel. Software abstractions: Logic, language, and analysis. Cambridge: MIT Press, 2006.

[Naur et al. 1960] Naur, Peter, ed., et al. Report on the Algorithmic Language ALGOL 60. Numerische Mathematik 2 (1960): 106-136. Also Communications of the ACM 3.5 (1960): 299-314. doi:https://doi.org/10.1145/367236.367262.

[Peirce 1906] Peirce, Charles Santiago Sanders. Prolegomena to an apology for pragmaticism. The Monist 16 (1906): 492-546. Reprinted vol. 4 of C. S. Peirce, Collected papers, ed. Charles Hartshorne and Paul Weiss (Cambridge, MA: Harvard University Press, 1931-58).

[Pike 1967] Pike, Kenneth L. Language in relation to a unified theory of the structure of human behavior. The Hague, Paris: Mouton, 1967.

[Wetzel 2008] Wetzel, Linda. 2008. Types and Tokens, in The Stanford Encyclopedia of Philosophy (Winter 2008 Edition), ed. Edward N. Zalta. Available on the Web at http://plato.stanford.edu/archives/win2008/entries/types-tokens/.

[Wetzel 2009] Wetzel, Linda. 2009. Types and tokens: On abstract objects. Cambridge, Mass., London: MIT Press, 2009.


[1] It may be worth noting that Peirce makes explicitly clear that blank spaces between words are also to be considered tokens of a specific type. The quoted paragraph continues as follows: The term (Existential) Graph will be taken in the sense of a Type; and the act of embodying it in a Graph-Instance will be termed scribing the Graph (not the Instance), whether the Instance be written, drawn, or incised. A mere blank place is a Graph-Instance, and the Blank per se is a Graph - but I shall ask you to assume that it has the peculiarity that it cannot be abolished from any Area on which it is scribed as long as that Area exists.

[2] We remain agnostic on the related question whether there can be types without associated tokens.

[3] The concept of occurrences is not without its own complications and subtleties, but we will not detain the reader with a discussion of them. A helpful discussion of the distinction between tokens and occurrences, and a useful summary of some of the related philosophical issues, may be found in [Wetzel 2008] and [Wetzel 2009], and also our discussion further below in section section “Types and tokens at different levels”.

[4] The notion of such spatially and temporally disjoint objects forming a single whole may trouble some readers, but consideration of such noun phrases as the Aleutian islands, the Olympic Games, and Poland may persuade such readers that some cases (at least) of temporal and physical disjointness seem to pass without comment.

[5] In Goodman's terms, no mark may belong to more than one character [Goodman 1976] p. 133.

[6] One outstanding difference should probably be mentioned: while Peirce explicitly contrasts the concrete token with the abstract type, the phones discussed by linguists and captured in phonetic transcriptions whether broad or narrow are not concrete sounds but abstract classes of sounds. This does not, however, seem to us to make the concept of phoneme irrelevant to our topic: like a type, a phoneme provides a unit which serves to make identical many things which would otherwise be distinct. It does not matter for our purposes whether those things are abstract phones or concrete segments of utterances.

[7] Other notations could serve the purpose as well; we choose Alloy because it has a reasonably clear, easily learnable logical notation and convenient, useful tools for checking the model. We offer no systematic introduction to Alloy syntax here; the reader is directed to the Alloy web site at http://alloy.mit.edu/ and to Jackson's book [Jackson 2006]. The reader unfamiliar with Alloy notation should be able to follow the essentials of the discussion, since every salient property of the model is stated both in Alloy and in English prose.

[8] For purposes of this paper, the identity of the type is not part of the identity of the token. If a particular mark is either an n or a u, then it is a token which is either of type n or of type u; the two different readings are different readings of the same token, not readings positing different tokens in the document. This allows two readers to disagree about which type is instantiated by a given token without requiring them also to disagree about the identity of the token in question.

[9] Note, however, that the arguments brought forward by Wetzel against the association of types with sets or classes may also apply with equal force to mereological sums [Wetzel 2009] (chapter 4, section 5).

[10] It is sometimes thought that the tokens of any given type necessarily resemble each other in some way (graphical or visual similarity in the case of written tokens, acoustic similarity in that of phonemes). But it seems to us unlikely that any measure of visual similarity could possibly be constructed that would group together all tokens of (for example) lower-case Latin letter g, and exclude all other objects. As far as we can tell, the only property tokens of a given type are guaranteed to have in common is that they instantiate that type. (One might indeed speculate that the concept of type was invented precisely to allow us to talk about these tokens as a group, since the instances of a type cannot by identified by appealing to any other property.) Independently, Goodman and Wetzel have come to the same conclusion; Wetzel devotes much of her chapter 3 to demolishing the view that tokens of a type must share some properties other than that of instantiating the type; see also [Goodman 1976], pp. 131 and 138.

[11] The model thus disallows the convention mentioned above, in which tokens are ordered but the order is taken as insignificant. It might be better to require only that ordered regions instantiate compound types.

[12] It might be desirable to single these lowest-level compound types and tokens out with a signature of their own, for example: 

sig Text_Flow extends S_Unit {
  types : seq Basic_Type
}{
  kind = PCData
  no children 
}
sig Token_Sequence extends Region {
  tokens : seq Basic_Token
}{
  type in Text_Flow
  type.types = tokens.@type
  no subregions
}
one sig PCData extends Kind {}
The overall system seems simpler, however, without this elaboration.

[13] It is tempting to suggest that the regions of a document partition the physical space of the text carrier [Cayless 2009], and in some simple cases they do. In the general case, however, the marks even of basic tokens may overlap with other marks constituting other tokens, and unwritten space in a document does not always constitute a token.

[14] We strive to use the term document always and only for physical objects, and the term text for the type instantiated by a document. This usage is not universal among those who speak and write about texts and documents.

[15] As the example illustrates, this proposal for disjunctive types arose in the context of work on the logic of transcription, but we believe it to be more generally applicable: it can be used to describe all cases of uncertainty, whether the document in question is being transcribed or not. The curious reader may wish to know that the correct literal transcription of the example is muuvnyzi, which is the secret-writing form of the German word offenbar public, apparent, obvious.

[16] Strictly speaking, in this case even the individuation of particular marks as constituting tokens differs in the two readings: the marks constituting a single token of the type y in one reading are, in the other reading, two tokens of f and i. The word tokens have different boundaries in the two directions. And so on. For now, our model ignores these complications; to address them directly it would seem to be necessary to model explicitly the marks which constitute tokens, and to indicate how different sets of marks are individuated now as one token and now as another. But it does not seem possible, in the general case, to treat marks as sets of individuals independent of particular readings of the marks: it is frequently only through being identified as a token of a particular type that marks can successfully be individuated and distinguished from each other. A similar (albeit aesthetically less interesting) example can be found in [Goodman 1976] pp. 138-139. Goodman's example has the property that there is no ambiguity about the organization of marks into tokens, and that the same token is intentionally written so that it can be assigned to several types.

[17] This is not strictly true: the formulation above includes constraints that enforce the parallel compositionality of tokens and types by requiring the types of a region's subregions to be the children of the region's type. These need to be reformulated to account for the presence of disjunctive and conjunctive types. In this paper, we simply ignore this complication.

Claus Huitfeldt

Associate Professor (førsteamanuensis)

Department of Philosophy, University of Bergen

Mag.art. Claus Huitfeldt (born 1957) is Associate Professor (førsteamanuensis) at the Department of Philosophy of the University of Bergen since 1994.

He was founding Director (1990-2000) of the Wittgenstein Archives at the University of Bergen, for which he developed the text encoding system MECS as well as the editorial methods for the publication of Wittgenstein's Nachlass — The Bergen Electronic Edition (Oxford University Press, 2000).

He was Research Director (2000-2002) of Aksis (Section for Culture, Language and Information Technology at the Bergen University Research Foundation). In 2003 he returned to his position at the Department of Philosophy, where he teaches modern philosophy and philosophy of language, and also gives frequent courses in text technology at the The Department of Humanistic Informatics.

He was active in the Text Encoding Initiative (TEI) since 1991, and was centrally involved in the foundation of the TEI Consortium in 2001. The consortium now counts more than 90 member institutions.

Huitfeldt's research interests are within philosophy of language, philosophy of technology, text theory, editorial philology and markup theory. He is currently leader of the project Markup Languages for Complex Documents (MLCD).

Yves Marcoux

Associate Professor

Université de Montréal

Yves Marcoux is a faculty member at EBSI, University of Montréal, since 1991. He is mainly involved in teaching and research activities in the field of document informatics. Prior to his appointment at EBSI, he has worked for 10 years in systems maintenance and development, in Canada, the U.S., and Europe. He obtained his Ph.D. in theoretical computer science from University of Montréal in 1991. His main research interests are document semantics, structured document implementation methodologies, and information retrieval in structured documents. Through GRDS, his research group at EBSI, he has been principal architect for the Governmental Framework for Integrated Document Management, a project funded by the National Archives of Québec and by the Québec Treasury Board.

C. M. Sperberg-McQueen

Black Mesa Technologies

C. M. Sperberg-McQueen is a consultant specializing in preserving and providing access to cultural and scientific data. He has served as co-editor of the XML 1.0 specification, the Guidelines of the Text Encoding Initiative, and the XML Schema Definition Language (XSDL) 1.1 specification. He holds a doctorate in comparative literature.