Introduction
Education content publishers increasingly distribute content to multiple delivery channels including printed textbooks, ebooks, Learning Management Systems (LMS's), and web-based Personal Learning Environments (PLE's). To better support new content multiple destination distribution requirements, education content publishers are increasingly moving to XML production workflows and implementing MathML as part of a larger digital evolution. Publishers traditionally competed by supplementing education programs and content with ancillary materials delivered as hard-copy, or increasingly, to an LMS as ebook content, or to a PLE capable of automatically grading homework assignments and quizzes. XML is a natural fit for storing large volumes of education content including MathML. However, education content publishers currently face a number of challenges and obstacles to author, edit, and distribute math content across delivery channels. This paper describes current trends in K-12 education content publishing and where MathML fits in through examples of how publishers currently address authoring, editorial, and production workflow obstacles.
Digital Content Revolution
Education publishers and libraries started down the path to digital content revolution as far back as the mid-1950s with the introduction of the Xerox machine. In 1956, the United States Congress approved the Library Services Act (later to be renamed the Library Services and Technology Act). This legislation provided public funding to libraries for exploring further use of computer-based systems to control bibliographic metadata and library catalogs. By 1960, the digital revolution to catalog and store full-text published documents was in progress, marking the beginning of the end for the Dewey Decimal System. The digital content revolution continued as libraries and educators swiftly adopted computers and databases to manage bibliographic metadata, library catalogs, and the distribution of scholarly periodical content. Library science in the last twenty years has become increasingly about what we can search for and access through a web browser. Benefits of the digital content revolution affect libraries and scholarly and education content publishers.[1]
In 2015, education content publishing, specifically K-12 content publishing, is at a turning point. More and more K-12 content is published and distributed as ebooks and in online environments as components of LMS's and PLE's than ever before. K-12 publishing is now in the very heart of the digital content revolution via the mass adoption of computers, the internet, web browsers, and ubiquitous devices capable of downloading and rendering content for student consumption. Distributing content, either scholarly content or K-12 education content, across the web, has become quite the problem, however.
XML and MathML
Educational publishers are moving to XML-based publishing production workflows and embracing MathML as part of the industry effort to make content available for both traditional print channels and digital delivery including ebooks. Furthermore, publishers are becoming more competitive by providing ancillary education content that often include web-based PLE's and adaptive learning systems.[2]
MathML was the very first XML-based markup specification, released in 1998.[3] Both scholarly and education content publishing communities immediately saw the value of MathML as the means to, at a minimum, markup math content for all the same reasons any other content is now marked up as XML. Reuse, repurposing, accessibility, and multiple distribution channels are common goals for implementing XML-based publishing production workflow systems. XML and MathML are a natural fit as a content source format, but scholarly and education content publishers face some very specific challenges to publishing math content marked up as MathML[4] including:
-
Lack of support for K-12 mathematical content, such as stacked equations, long division, geometry and visual mathematical representations (e.g., diagrams, charts, number lines).
-
Lack of annotation support. K-12 math examples often contain associated line-by-line annotations intended to walk students through problem-solving.
-
Government regulated accessibility requirements specific to K-12 content, and the lack of quality assistive technology tool support.
-
Inconsistent adoption and support for MathML across platforms in web browsers and reading devices and apps.
-
Adaptive technology maturity. Adaptive learning scenarios currently only support very simple automation such as choosing what content to display based on a student's answer (e.g., multiple choice).
Current Trends in Education Content Publishing
Most industries have been affected in some part by the digital content revolution (or the movement of content and publishing production workflow processes into digital formats) currently underway, and possibly none more so than education content publishing. Sales of physical textbooks and other learning materials account for 70% of education content publishers’ revenue. Digital content formats now account for 20% of revenue, and bundles, which usually include a software or web component in addition to a textbook, make up 10% of revenue.[5]
Digital content formats have seen a 201% revenue growth since 2009. This upward trend will likely continue as educators realize the flexibility they have to customize and configure digital content. Digital content formats not only cover ebooks and audiobooks but also what might be considered services, including ancillary material such as question banks and videos. With a recent general decline in education textbook revenues due to shrinking school budgets, the education publishing landscape has become more competitive, and publishers are stepping up by offering a wider range of options for educators. These days, K-12 teachers and curriculum planners can customize student textbooks to match curricula focus, or quickly modify learning materials to accommodate unique needs of their particular classrooms and students.
As part of the trend towards personalized learning, technology companies are teaming up with education publishers to develop new technology systems driven by adaptive learning. Adaptive learning is a term used for adapting lesson or assessment content to an individual student based on observations of how the student responds to what he or she is learning. For example, if a student grasps a concept quickly, the next concept can be presented without boring the student. If a student struggles with a concept, time can be spent reinforcing the specific material. Web-based platform providers often use an assessment-driven approach as the conditional choices made by adaptive learning-enabled systems. The software compares responses to a benchmark while students work through exercises. The software algorithmically adjusts remaining exercises in real time, reflecting the student's current rate of topic mastery. Education technology companies are working to make further advances in this area, and publishers are already adding adaptive learning platforms to their products. Houghton Mifflin Harcourt’s partnership with Knewton is one example of a publisher serving the K-12 market with adaptive learning materials.[6]
MathML Content Production Challenges
Though the file storage format for mathematical content has for the most part been settled by adopting MathML in publishing workflows, education content publishers face a number of obstacles when delivering mathematics as part of their digital offerings. Mathematical typesetting is a tricky beast - often compared to "dark arts" by publishers and production experts alike. Unlike images, which are often used to enhance or supplement the text, mathematics is an integral part of the content and loaded with meaning. Furthermore, the visual layout of a formula must be precise, as this is part of the mathematical content's meaning. Finally, mathematical equations are often expressed with vertical and horizontal layouts. Taken together rendering formulae is a complex challenge. Despite the fact that MathML is an eighteen-year-old specification, the level of complexity required to maintain semantic meaning through both layouts and numeric content has hindered education publishers' adoption efforts. But education content publishers are now more motivated than ever to adopt MathML now that the W3C and IDPF formally included MathML as part of the HTML5 and EPUB specifications.
It is in this new digital context that education content publishers are expanding into new frontiers with digital content but encounter obstacles in math content publishing production workflows.
Inconsistent MathML Support in Authoring Tools, Web Browsers, and Digital Reading Devices and Apps
Despite the fact that MathML is part of both the HTML5 and EPUB 3 specifications, web browsers and ereading devices and apps are notorious for inconsistent MathML support. For example, Amazon's Kindle devices and software, the most popular ereading devices and software in the United States, do not support MathML. K-12 math content publishers must support constructs unique to K-12 education not widely supported in MathML publishing production workflow tools including authoring and rendering software. Further, K-12 math content must also meet accessibility regulations, but publishing production staff often have trouble convincing management to provide resources required to satisfy regulations in the face of sometimes conflicting business priorities.
The elevation to recommendation status of the IDPF EPUB 3 and W3C HTML5 specifications respectively in 2011 and 2014 ushered in an exciting new era of enhanced content. Both specifications now allow the inclusion of various types of media and the potential for creating enhanced and interactive digital content has exploded. Ebooks and web pages may include video footage, music clips, or small software applications, just to name a few media options. EPUB 3 and HTML5 both may also include MathML, opening new horizons for publishing mathematical content. For instance, imagine seeing an equation in a trigonometry etextbook describing a sine curve, tapping or clicking the equation, and watching the graph of the equation appear with adjustable parameters.
Education content publishers are poised to take advantage of the new specification capabilities. Unfortunately, MathML support remains inconsistent across both web browsers and ereading devices and apps. Most ereading software in today's market relies heavily on browser technology. MathML support in ereading devices and apps may coincide with support in browser rendering engines, which is the case with Apple's WebKit-based Safari web browser, and the Apple iBooks reading app for iOS and OS X. However, the WebKit browser rendering engine only supports a limited portion of MathML 2.0. Apple's Safari web browser and iBooks can display MathML to some extent on both iOS and OS X, but the current level of support is not acceptable for production publishing K-12 math content.
In contrast, Mozilla's Gecko rendering engine, which is the basis for the Firefox web browser, has the most extensive MathML implementation of any web browser to date. Google removed all support for MathML from the proprietary Blink web rendering engine in 2013 after announcing the company's intention to move away from WebKit as the basis for Google's Chrome browser.[7][8] Moreover, despite Microsoft’s recent stance toward embracing open standards and the addition of limited support for MathML in Microsoft Office, Internet Explorer does not support MathML. In fact, Microsoft currently has no plans to implement MathML in Edge, their latest web browser and Internet Explorer's successor.[9]
Peter Krautzberger (Manager, MathJax Consortium) suggested in an O'Reilly Radar blog post that the volunteer nature of web browser rendering engine development is a reason the rendering engine development community has not adopted MathML more widely.[10] Krautzberger notes that Mozilla and WebKit both relied upon volunteer developers to implement and test MathML implementations. However, volunteers are often tasked with multiple projects in addition to developing commercial software. It is not practical for math content publishers to continue to rely on volunteer effort. Volunteers may come and go, leaving no one accountable for the results left behind, and possibly no one to implement requirements that didn't make it into the web browser engines in the first place.
The current state of MathML support in web browsers does not preclude future progress. Mozilla currently supports significant portions of MathML 2.0 and 3.0. Webkit is close to supporting 80% of the specifications. Conspicuously missing from both engines, however, is support for elementary MathML constructs: long division, stacked equations, and K-12 specific visual features (e.g., number lines and various graphs).
As evidenced by the growing support of MathML in software adhering to the EPUB 3[11] and HTML 5[12] specifications, MathML implementation and support will eventually be available across web browsers, ereading devices, and apps. All of the major browser rendering engine vendors and many ereading device and app developers directly contributed to both the development of the EPUB 3 and HTML5 specifications. The IDPF and W3C officially approved including MathML in the recommended specifications. However, until browsers and ereaders can render MathML natively, MathJax, an open source cross-platform Javascript library for rendering MathML, is available as an interim solution.
MathJax is a powerful JavaScript library capable of rendering complex LaTeX as images, or where possible, as MathML. However, MathJax must modify a web page's DOM. In doing so, MathJax rendering can potentially interfere with other libraries and tools that access the DOM. For example, a braille display that works with iOS may no longer be able to decipher MathML if MathJax settings render math as images due to configuration or browser capability. MathJax fills the gap created by absent MathML support in web browser rendering engines. MathJax also enables scholars and publishers to create math content in LaTeX or MathML. The library has many configuration options and has been adopted by scholarly societies, and ereading application developers alike. However, MathJax has a learning curve that developers must address when integrating the library into applications and platforms. Developers often encounter performance issues that must be worked around through specific configurations. Furthermore, the range of possible MathJax configurations combined with a market where developers no longer know what screen or device will be used to read content creates a QA risk requiring further investment to mitigate. Therefore, while MathJax provides a mature solution for publishing math on the web and in digital content, development and configuration required to integrate MathJax requires extra "care and feeding" to maintain application integrations. In the end, the best solution for rendering and displaying math on the web and in digital content is still native MathML support in browsers and ereading devices and apps. Native MathML in web browsers requires maintenance and development on the part of browser rendering engine developers, instead of with the scholarly and education community, who would much rather be writing math than web browser application code.
Math Requirements Specific to K-12 Education Content
Educators explain sometimes difficult concepts to young minds, and this task is often best accomplished visually. K-12 math textbooks include a large number of diagrams, graphs, fill-in-the-blanks, and stacked expressions to teach early math concepts. See Figure 1 for an example showing a stacked subtraction operation with carry-overs, borrowing, and foreground colors to explain large subtraction operations. Presentation-based MathML markup for all figures in this section is included in Appendix A.
Figure 1: Stacked Subtraction with Borrowing and Carry-Overs

Figure 2: Stacked addition, Fractions
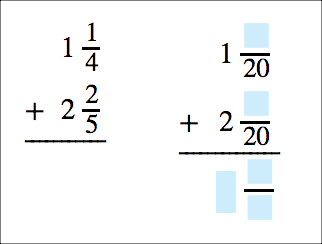
Figure 3: Fill-in-the-Blank Elementary Math Equations

Figure 4: Leveled 2-digit stacked exercise problems
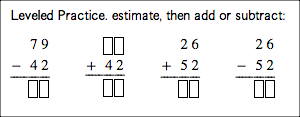
MathML 3.0 added new features to support elementary math notation, which gets educational publishers part of the way towards a solution for these more complex structures. The problem is that since elementary math notation is not widely used by scholarly authors and in higher education, tools have been slow to add support for it. To address problems with consistency in tool support of MathML, content creators often have to resort to using the MathML 2.0 approach for encoding equations. For the stacked subtraction example above, this means using tables and other tweaks. However, the MathML specification working group had good reason to add elementary math notation to MathML 3.0 - without it, authors have to make too many manual adjustments to the MathML to get it to display properly. Furthermore, MathML 2.0 lacks the semantic information required by assistive technology to properly render elementary math for students with special needs.
Figure 5: Long Division with 3 summation lines and cyan fill-in-the-digit spaces
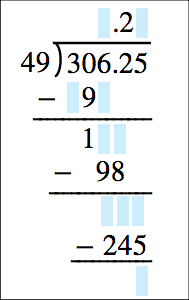
Figure 6: Long Division Exercise with fill-in-the-blank digits
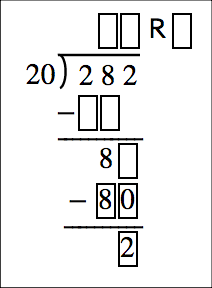
Once again, we have a situation where tool development must catch up with specification capabilities. However, even if there were complete web browser implementations of the MathML 3.0 specification, publishers still have a problem with heavily image based teaching approaches specific to K-12 math. There is no MathML markup, for example, to display a number line demonstrating how to add or subtract with negative numbers. Therefore, some subject matter experts argue that the highly visual elements of K-12 textbooks still beyond the scope of the current MathML specification were never considered in the first place. The general conclusion of these subject matter experts is that no implementation should happen before the topic can be revisited and prioritized by the MathML working group for inclusion in a future version of the MathML specification. We do not think this is a practical approach to the implementation problem and the fact that current solutions disenfranchise thousands of kids from accessing existing math content due to digital content accessibility support issues. Authoring and rendering solutions that can support unique K-12 math constructs can be a combination of W3C standards: MathML, SVG, and Annotations exist right now.
A combination of MathML and the upcoming W3C Web Annotations specification may be suitable for some K-12 math only requiring basic rendering and annotations. However, for purposes of interactive content delivery, publishers must still rely on rendering math as SVG images. Publishers who wish to publish K-12 math content heavily designed and requiring vector image implementations not currently supported by the existing MathML specification may require a combination rendering implementation of MathML, SVG, and Web Annotations standards together.
The K-12 education publishing community will finally realize a pie-in-the-sky solution when MathML, SVG, and W3C Annotations are mature enough and combined to create labeled graphs and equations while retaining the underlying overall advantages of MathML solutions. Specifically, distributed digital content that is accessible and rendered properly in native apps, and devices, as well as the open web platform. The requirement to combine MathML, SVG, and W3C Annotations to create the most inclusive support for K-12 math is one reason we continue to advocate for native MathML support in web browsers and ereading devices and apps.
An additional issue to the K-12 education publishing community is the lack of support for annotating math concepts in worked through problems with MathML markup as demonstrated in Figure 7.
Figure 7

Accessibility
MathML enables education content publishers to produce content conformant with governmental accessibility regulations. MathML is the standard of choice for the accessibility community because of its detailed description of mathematical expressions. With the level of detail provided by MathML, a mathematical expression can be converted to braille, narrated, or navigated by assistive technology in a way that students with special needs can comprehend.
In 1974, the U.S. Department of Education established the Federal Individuals with Disabilities Education Act (IDEA) to provide special services enhancing the education of students with disabilities. The U.S. Department of Education provides format guidelines for states and local school districts for creating accessible content. The Department of Education recommends that educational publishers provide materials in the NIMAS format, which is a national accessible K-12 textbook standard. NIMAS, and other accessibility standards including DAISY, a standard for digital talking books, and PDF/UA (accessible PDFs), require mathematical content to be coded as MathML.
Although the standards are in place for encoding math content, it is less clear to education content publishers how to implement accessibility specifications such that students have the freedom to use their assistive technology tools of choice. For example, the popular JAWS screen reading software recently added support for MathML, but only within Microsoft Internet Explorer. Further, the implementation is MathJax dependent. However, as previously mentioned, MathJax may interfere with assistive technology by modifying the underlying web page structure. The number of potential assistive technology tools such as braille readers and other screen readers is directly affected if content providers choose to support the MathML-enabled JAWS screen reading software.
Publishers currently use tools such as MathSpeak from gh, LLC, MathML Cloud from Benetech, or MathFlow Equation Composer from Design Science to render MathML as Text-to-Speech. Screen readers that are not MathML "aware" may then read the rendered Text-to-Speech content. Figure 8 shows the Text-to-Speech used as alternative text for the quadratic formula. Using a third party tool to render MathML for screen readers is a solution that is less than ideal. First, it limits students in the tools that they can use. For example, Text-to-Speech renditions are phonetic and, therefore, useless to a braille translation system. Secondly, without the ability to read MathML directly, screen readers are not truly rendering MathML. Studies have shown that students with learning disabilities benefit from a different reading style than blind students. If speech text is hard-coded for the screen reader, no room is left for customizing math speech to specific student requirements.
Figure 8: Text to Speech Quadratic Equation
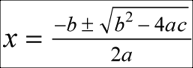 |
| x equals . fraction negative b , plus minus . square root of b squared , minus . 4 eh c end root , over 2 eh end fraction |
Case Study: Accessible MathML and Personal Learning Environments
Our commitment is to making digital solutions that are usable by the widest range of students, with or without disabilities.
To fulfilling our continued commitment to accessibility, this is the first step in moving the dial towards better accessibility of math content. This first step of authoring math content using MathML is the ideal solution.
-
Education content publisher with approximately 60 math titles available in proprietary PLE product as ebooks.
-
All books contain MathML and corresponding rendered images.
-
Use Case: Presentation MathML and make it accessible to screen readers within the personal learning environment portal.
-
Display Solution: MathJax to display MathML. Images for really complex math where required.
-
Accessibility Solution: MathSpeak from gh, LLC. to generate screen readable alt text for each MathML instance. Bolt screen readable alt text descriptions back on to MathML and related images in portal.
-
Current Status: Implementation is in progress and ongoing. Publisher's MathML is structured correctly in order to have gh, LLC. generate screen readable alt text descriptions.
Adaptive Learning
One of the appeals of purchasing digital content for school districts is the opportunity to free up teaching staff time with automation. Publishers often make an item bank available from which staff can draw for exams and homework assignments. Some e-learning vendors, such as Madeira Station with its Cognero assessment system, can even go so far as dynamically generating mathematical expressions and graphs with a variable substitution scheme.
On the opposite end, educators are also interested in automated grading of homework assignments, quizzes, and exams. For multiple choice questions, this is easily done, but as students enter upper-level mathematics, where students must provide exercise answers that are an equation, this becomes more difficult. Currently, most assessment systems are limited to string comparisons, however. The expectation for the future is for developers to enhance and grow automatic assessment systems alongside adaptive learning technology adoption.
In 2015, Adobe Flash has been all but replaced by HTML5-based web applications in Learning Management Systems that support content, assessment, and assessment-based adaptive learning that must also support accessibility requirements and regulations. To this end, K-12 publishers have retooled and re-engineered the publishing production workflows required to support systems that automatically prompt students to review material or present additional assessment questions based on previous answers. Much of the retooling and changes to workflow are straightforward: Move content publishing production workflows away from reliance on proprietary file formats and tools. Maintain source content in open, markup-based formats enabling the reuse of content in print books and digital, HTML5-based delivery formats including ebooks and web-based LMS's and PLE's.
Moving to markup-based formats enables publishers to easily render education content to teach children how to read and spell. Math, however, despite being a full-fledged HTML5 citizen, became a sticky issue for publishers to resolve in adaptive learning scenarios. Making web-based math problems work in an adaptive learning environment requires software that can intelligently read metadata and content in order to determine whether the student has correctly solved the problem and what problem to show next. Enabling adaptive learning systems to determine whether or not a math problem has been answered correctly and what content to show next requires problems to be marked up such that software can correctly interpret student responses and process metadata to determine what content to display based on the response. Figure 9 demonstrates a math problem that, if rendered as an image, is effectively invisible to adaptive learning systems.
Figure 9: Two digit stacked subtraction problem rendered in IXL's Interactive web-based practice application[13]
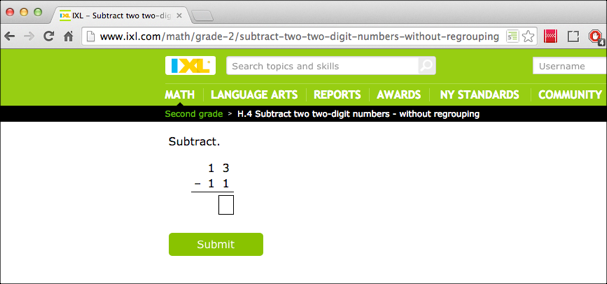
Educational publishers have been publishing K-12 math as images with associated alternative text for years due to the lack of MathML support in publishing systems and web browsers. The "image plus alternative text" approach does not meet the requirements of today's adaptive learning technology which requires both the math problem and associated metadata to be marked up for machine readability and the logic of adaptive learning systems.
How the Education Publishing Community Can Help
Despite the problems with moving K-12 math content into the digital realm, we have reason to be optimistic. The standards are in place, MathML rendering software exists, is continually improving, and in many cases developments are already underway to improve the landscape for mathematical communications across the board. Education publishers and subject matter experts can help by advocating for and supporting MathML authoring tool and rendering engine development efforts.
The easiest action education content publishers can take is to let browser and ereader device manufacturers know the importance of MathML to children’s education. When browsers, apps, and ereaders support MathML natively, a range of opportunities will open to not just publishers, educators, and students, but to anyone who needs to convey mathematical information electronically.To start, both Google and Microsoft have forums on which education publisher staff and subject matter experts can register to express interest in support for MathML in Chrome and Edge, Microsoft's Internet Explorer successor, respectively.
A deeper dialog needs to happen to convince browser and ereader vendors to invest in MathML development. Education publishers and other elearning software providers can help by providing incentives and grassroots support to initiate a dialog with web browser product management teams. The United States Justice Department has filed lawsuits against organizations failing to implement accessibility legislation in the United States. For the most part, these lawsuits have been limited to universities.[14] Precedence now exists for a more litigious approach to forcing the publishing industry and other media entities to comply with accessibility legislation. edX, a provider of Massive Open Online Courses (MOOCs), was forced to settle a complaint alleging violations of the Americans with Disabilities Act filed by the United States Justice Department in April 2015.[15]
Developers should consider contributing support to MathML by using tools to write and implement the specification. One of the greatest benefits of supporting open standards is that what works in one application will (or should) work in another application. Developers can actively prevent disenfranchisement of the overall content audience by adding support for native MathML to both native- and web-based applications and by integrating open source programs and solutions.
Subject matter experts, developers, and publishing companies may also consider contributing to projects directly supporting MathML development.Open source projects that could benefit from both developer and financial contributions to the Gecko and WebKit web browser engines as well as the MathJax JavaScript library project.
Conclusion
Education publishers are responding to the combined pressures of decreased spending in school districts and increased competition by innovating product and service offerings. In addition to traditional print textbooks, education publishers provide ebooks and other digital content. Digital content delivery formats pave the way for new enhanced educational experiences with video, software, and interactive media. Furthermore, digital content delivery formats, especially markup-based formats, can be adapted to the needs of a particular district or student. In the United States, federal and state law states require all content, including K-12 math content to comply with accessibility legislation.
Publishers continue to face progress-blocking roadblocks when it comes to publishing K-12 math content in both native apps and on the open web:
-
Although MathML is a natural encoding format for math content in education, tool support is lagging for K-12 math constructs in general.
-
Although MathML is part of both the HTML5 and EPUB 3 specifications, browser and device vendors do not yet consistently support MathML.
-
K-12 publishers must support math constructs that are unique to lower level math content and which are not supported by the MathML 3 specification despite the added support for very basic and minimal elementary math notation.
-
MathML rendering engines have varying levels of support for MathML 3.0.
Education publishers of K-12 math content continue to make do with less-than-ideal solutions despite existing implementation and adoption issues. The polyglot MathJax JavaScript library is used widely to support rendering and displaying mathematical content in both web browsers and apps driven by web browser rendering engines. For elementary math notation, some publishing production editorial teams currently use a combination of MathML 2 with tweaks and hacks specifically designed to render across browsers through MathJax. Ideally, these production teams will modify their workflows and current hacks when the MathML 3-based elementary math components are supported in editing apps and rendering engines. Publishers are also tackling the onerous and time-consuming task of producing alternative text for rendition by screen readers to target a subset of assistive software.
The future looks bright for open web standards-based mathematical communication in theory. Native app and web-based mathematical communication success are heavily dependent on the need for dialog. Recommended participants in this required dialog include education content provider representatives, members of web browser rendering engines' product management community, and members of the W3C MathML working group. This dialog has yet to occur. That said, MathML-based solution advocates and subject matter experts continue to advocate for the implementation and support of delivering accessible and complicated math content across multiple rendition formats including native apps and the open web. MathML specification and accessibility advocates continue to encourage publishers to start the necessary dialog with web browser rendering engine product developers. The purpose of the dialog is to discuss further the overall publishing use cases for implementing MathML natively, as part of all web browser rendering engines.
The outcome of this dialog will be a better understanding of the financial and implementation resource requirements necessary to render all levels of math, including K-12 math, for anyone who wishes to learn. Supporting MathML across apps and the open web is not a matter of missing parts; it is a matter of prioritization. No manager will prioritize a potentially expensive development endeavor without understanding exactly where the functionality must exist within company priorities. Ideally, managers should prioritize supporting accessible and complicated math content for all users across a variety of digital formats. Litigation should be a last resort to force a company's hand to do the right thing rather than the source of re-evaluating business goals and management priorities.
Appendix A. MathML Markup Examples
MathML Markup for Figure 1
<math>
<mrow>
<mstyle mathvariant='sans-serif'>
<mrow>
<mtext>3 col worked out subtract, carryovers, crossouts, sum </mtext>
<mspace indentalign='left' linebreak='newline'/>
<mtext>and mpadded in top row, 2nd col:</mtext>
<mspace linebreak='newline' indentalign='left'/>
</mrow>
</mstyle>
<mspace indentalign='left' linebreak='newline'/>
<mtable align='top' columnspacing='0em' rowspacing='1ex, -.5ex'>
<mtr>
<mtd></mtd>
<mtd>
<mover>
<mrow>
<menclose notation='updiagonalstrike'>
<mstyle>
<mrow>
<mn>3</mn>
</mrow>
</mstyle>
</menclose>
</mrow>
<mrow>
<mstyle mathcolor='#da2128'>
<mrow>
<mn>2</mn>
</mrow>
</mstyle>
</mrow>
</mover>
</mtd>
<mtd>
<mover>
<mrow>
<menclose notation='updiagonalstrike'>
<mstyle>
<mrow>
<mpadded height='-.2ex'>
<mrow>
<mn>0</mn>
</mrow>
</mpadded>
</mrow>
</mstyle>
</menclose>
</mrow>
<mrow>
<mover>
<mrow>
<menclose notation='updiagonalstrike'>
<mstyle>
<mrow>
<mn>10</mn>
</mrow>
</mstyle>
</menclose>
</mrow>
<mrow>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
<mstyle mathcolor='#da2128'>
<mrow>
<mn>9</mn>
</mrow>
</mstyle>
</mrow>
</mover>
</mrow>
</mover>
</mtd>
<mtd>
<mover>
<mrow>
<menclose notation='updiagonalstrike'>
<mstyle>
<mrow>
<mn>5</mn>
</mrow>
</mstyle>
</menclose>
</mrow>
<mrow>
<mstyle mathcolor='#da2128'>
<mrow>
<mn>15</mn>
</mrow>
</mstyle>
</mrow>
</mover>
</mtd>
</mtr>
<mtr>
<mtd>
<mo>−</mo>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mtd>
<mtd>
<mstyle mathcolor='#da2128'>
<mrow>
<mn>1</mn>
</mrow>
</mstyle>
</mtd>
<mtd>
<mstyle mathcolor='#da2128'>
<mrow>
<mn>7</mn>
</mrow>
</mstyle>
</mtd>
<mtd>
<mstyle mathcolor='#da2128'>
<mrow>
<mn>8</mn>
</mrow>
</mstyle>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<mo>_</mo>
</mrow>
</mtd>
<mtd>
<mrow>
<mo>_</mo>
</mrow>
</mtd>
<mtd>
<mrow>
<mo>_</mo>
</mrow>
</mtd>
<mtd>
<mrow>
<mo>_</mo>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mphantom>
<mrow>
<mo>−</mo>
<mn>0</mn>
</mrow>
</mphantom>
</mtd>
<mtd>
<mstyle mathcolor='#da2128'>
<mrow>
<mn>1</mn>
</mrow>
</mstyle>
</mtd>
<mtd>
<mstyle mathcolor='#da2128'>
<mrow>
<mn>2</mn>
</mrow>
</mstyle>
</mtd>
<mtd>
<mstyle mathcolor='#da2128'>
<mrow>
<mn>7</mn>
</mrow>
</mstyle>
</mtd>
</mtr>
</mtable>
</mrow>
</math>
MathML Markup for Figure 2
<math>
<mrow>
<mtable align='top, 3' columnspacing='0em' rowspacing='1ex, .5ex'>
<mtr>
<mtd></mtd>
<mtd>
<mrow>
<mn>1</mn>
<mspace width='-.1em'/>
<mo></mo>
</mrow>
<mrow>
<mstyle displaystyle='false' mathsize='100%'>
<mrow>
<mstyle mathsize='130%'>
<mrow>
<mfrac>
<mrow>
<mn>1</mn>
</mrow>
<mrow>
<mn>4</mn>
</mrow>
</mfrac>
</mrow>
</mstyle>
</mrow>
</mstyle>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mo>+</mo>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mtd>
<mtd>
<mrow>
<mn>2</mn>
<mspace width='-.1em'/>
<mo></mo>
</mrow>
<mrow>
<mstyle displaystyle='false' mathsize='100%'>
<mrow>
<mstyle mathsize='130%'>
<mrow>
<mfrac>
<mrow>
<mn>2</mn>
</mrow>
<mrow>
<mn>5</mn>
</mrow>
</mfrac>
</mrow>
</mstyle>
</mrow>
</mstyle>
</mrow>
</mtd>
</mtr>
<mtr rowalign='top'>
<mtd>
<mrow>
<mo>_</mo>
</mrow>
</mtd>
<mtd>
<mrow>
<mo>_</mo>
</mrow>
</mtd>
</mtr>
</mtable>
<mspace depth='0.0ex' height='0.0ex' width='2em'/>
<mtable align='top' columnspacing='0em' rowspacing='1ex, -.5ex'>
<mtr>
<mtd></mtd>
<mtd>
<mrow>
<mn>1</mn>
<mspace width='-.1em'/>
<mo></mo>
</mrow>
<mrow>
<mstyle displaystyle='false' mathsize='100%'>
<mrow>
<mstyle mathsize='130%'>
<mrow>
<mfrac>
<mrow>
<mi class='MathML-Blank' mathsize='140%' mathcolor='#c7eafb' mathvariant='normal'>■</mi>
</mrow>
<mrow>
<mn>20</mn>
</mrow>
</mfrac>
</mrow>
</mstyle>
</mrow>
</mstyle>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mo>+</mo>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mtd>
<mtd>
<mrow>
<mn>2</mn>
<mspace width='-.1em'/>
<mo></mo>
</mrow>
<mrow>
<mstyle displaystyle='false' mathsize='100%'>
<mrow>
<mstyle mathsize='130%'>
<mrow>
<mfrac>
<mrow>
<mi class='MathML-Blank' mathsize='140%' mathcolor='#c7eafb' mathvariant='normal'>■</mi>
</mrow>
<mrow>
<mn>20</mn>
</mrow>
</mfrac>
</mrow>
</mstyle>
</mrow>
</mstyle>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<mo>_</mo>
</mrow>
</mtd>
<mtd>
<mrow>
<mo>_</mo>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mphantom>
<mrow>
<mo>+</mo>
<mn>0</mn>
</mrow>
</mphantom>
</mtd>
<mtd>
<mrow>
<mtext> </mtext>
<mspace class='MathML-Blank' width='.6em' height='2ex' depth='1ex' mathbackground='#c7eafb'/>
<mtext> </mtext>
<mspace width='-.1em'/>
<mo></mo>
</mrow>
<mrow>
<mstyle displaystyle='false' mathsize='100%'>
<mrow>
<mstyle mathsize='130%'>
<mrow>
<mfrac>
<mrow>
<mi class='MathML-Blank' mathsize='140%' mathcolor='#c7eafb' mathvariant='normal'>■</mi>
</mrow>
<mrow>
<mi class='MathML-Blank' mathsize='140%' mathcolor='#c7eafb' mathvariant='normal'>■</mi>
</mrow>
</mfrac>
</mrow>
</mstyle>
</mrow>
</mstyle>
</mrow>
</mtd>
</mtr>
</mtable>
</mrow>
</math>
MathML Markup for Figure 3
<math>
<mrow>
<mstyle mathvariant='sans-serif'>
<mrow>
<mtext>Write a number that makes the equation true:</mtext>
<mspace indentalign='left' linebreak='newline'/>
</mrow>
</mstyle>
<mn>5</mn>
<mo>+</mo>
<mn>5</mn>
<mo>=</mo>
<mn>2</mn>
<mo>+</mo>
<menclose class='MathML-Blank' notation='box'>
<mrow>
<mpadded height='.9em' width='1.5em' depth='.4em' lspace='.57em'>
<mrow>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mrow>
</mpadded>
</mrow>
</menclose>
<mspace indentalign='left' linebreak='newline'/>
<mn>5</mn>
<mo>+</mo>
<mn>5</mn>
<mo>=</mo>
<menclose class='MathML-Blank' notation='bottom'>
<mrow>
<mpadded height='1.25em' depth='.1em'>
<mrow>
<mspace width='1em'/>
<mphantom mathsize='160%'>
<mrow></mrow>
</mphantom>
<mspace width='1em'/>
</mrow>
</mpadded>
</mrow>
</menclose>
<mo>+</mo>
<mn>2</mn>
<mspace indentalign='left' linebreak='newline'/>
<mn>3</mn>
<mo>+</mo>
<mn>4</mn>
<mo>=</mo>
<menclose class='MathML-Blank' notation='box'>
<mrow>
<mpadded height='.9em' width='1.5em' depth='.4em' lspace='.57em'>
<mrow>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mrow>
</mpadded>
</mrow>
</menclose>
<mo>⁢</mo>
<mo>+</mo>
<mn>1</mn>
<mspace indentalign='left' linebreak='newline'/>
<mn>5</mn>
<mo>+</mo>
<mn>2</mn>
<mo>=</mo>
<mn>1</mn>
<mo>+</mo>
<menclose class='MathML-Blank' notation='bottom'>
<mrow>
<mpadded height='1.25em' depth='.1em'>
<mrow>
<mspace width='1em'/>
<mphantom mathsize='160%'>
<mrow></mrow>
</mphantom>
<mspace width='1em'/>
</mrow>
</mpadded>
</mrow>
</menclose>
<mspace indentalign='left' linebreak='newline'/>
<mn>8</mn>
<mo>−</mo>
<mn>4</mn>
<mo>=</mo>
<menclose class='MathML-Blank' notation='bottom'>
<mrow>
<mpadded height='1.25em' depth='.1em'>
<mrow>
<mspace width='1em'/>
<mphantom mathsize='160%'>
<mrow></mrow>
</mphantom>
<mspace width='1em'/>
</mrow>
</mpadded>
</mrow>
</menclose>
<mo>+</mo>
<mn>4</mn>
</mrow>
</math>
MathML Markup for Figure 4
<math>
<mstyle displaystyle='true'>
<mrow>
<mstyle mathvariant='sans-serif'>
<mrow>
<mtext>Leveled Practice. estimate, then add or subtract:</mtext>
<mspace indentalign='left' linebreak='newline'/>
</mrow>
</mstyle>
<mtable align='top' columnspacing='0em' rowspacing='1ex, -.5ex'>
<mtr>
<mtd></mtd>
<mtd>
<mn>7</mn>
</mtd>
<mtd>
<mn>9</mn>
</mtd>
</mtr>
<mtr>
<mtd>
<mo>−</mo>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mtd>
<mtd>
<mn>4</mn>
</mtd>
<mtd>
<mn>2</mn>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<mo>_</mo>
</mrow>
</mtd>
<mtd>
<mrow>
<mo>_</mo>
</mrow>
</mtd>
<mtd>
<mrow>
<mo>_</mo>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mphantom>
<mrow>
<mo>−</mo>
<mn>0</mn>
</mrow>
</mphantom>
</mtd>
<mtd>
<menclose class='MathML-Blank' notation='box'>
<mrow>
<mpadded height='-.2ex' depth='.2ex' lspace='-.2em' width='.1em'>
<mrow>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mrow>
</mpadded>
</mrow>
</menclose>
</mtd>
<mtd>
<menclose class='MathML-Blank' notation='box'>
<mrow>
<mpadded height='-.2ex' depth='.2ex' lspace='-.2em' width='.1em'>
<mrow>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mrow>
</mpadded>
</mrow>
</menclose>
</mtd>
</mtr>
</mtable>
<mspace depth='0.0ex' height='0.0ex' width='2em'/>
<mtable align='top' columnspacing='0em' rowspacing='.38ex, -.75ex, -.5ex, -.5ex'>
<mtr>
<mtd></mtd>
<mtd>
<menclose class='MathML-Blank' notation='box'>
<mrow>
<mpadded height='-.2ex' depth='.2ex' lspace='-.2em' width='.1em'>
<mrow>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mrow>
</mpadded>
</mrow>
</menclose>
</mtd>
<mtd>
<menclose class='MathML-Blank' notation='box'>
<mrow>
<mpadded height='-.2ex' depth='.2ex' lspace='-.2em' width='.1em'>
<mrow>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mrow>
</mpadded>
</mrow>
</menclose>
</mtd>
</mtr>
<mtr>
<mtd>
<mo>+</mo>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mtd>
<mtd>
<mn>4</mn>
</mtd>
<mtd>
<mn>2</mn>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<mo>_</mo>
</mrow>
</mtd>
<mtd>
<mrow>
<mo>_</mo>
</mrow>
</mtd>
<mtd>
<mrow>
<mo>_</mo>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mphantom>
<mrow>
<mo>+</mo>
<mn>0</mn>
</mrow>
</mphantom>
</mtd>
<mtd>
<menclose class='MathML-Blank' notation='box'>
<mrow>
<mpadded height='-.2ex' depth='.2ex' lspace='-.2em' width='.1em'>
<mrow>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mrow>
</mpadded>
</mrow>
</menclose>
</mtd>
<mtd>
<menclose class='MathML-Blank' notation='box'>
<mrow>
<mpadded height='-.2ex' depth='.2ex' lspace='-.2em' width='.1em'>
<mrow>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mrow>
</mpadded>
</mrow>
</menclose>
</mtd>
</mtr>
</mtable>
<mspace depth='0.0ex' height='0.0ex' width='2em'/>
<mtable align='top' columnspacing='0em' rowspacing='1ex, -.5ex'>
<mtr>
<mtd></mtd>
<mtd>
<mn>2</mn>
</mtd>
<mtd>
<mn>6</mn>
</mtd>
</mtr>
<mtr>
<mtd>
<mo>+</mo>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mtd>
<mtd>
<mn>5</mn>
</mtd>
<mtd>
<mn>2</mn>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<mo>_</mo>
</mrow>
</mtd>
<mtd>
<mrow>
<mo>_</mo>
</mrow>
</mtd>
<mtd>
<mrow>
<mo>_</mo>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mphantom>
<mrow>
<mo>+</mo>
<mn>0</mn>
</mrow>
</mphantom>
</mtd>
<mtd>
<menclose class='MathML-Blank' notation='box'>
<mrow>
<mpadded height='-.2ex' depth='.2ex' lspace='-.2em' width='.1em'>
<mrow>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mrow>
</mpadded>
</mrow>
</menclose>
</mtd>
<mtd>
<menclose class='MathML-Blank' notation='box'>
<mrow>
<mpadded height='-.2ex' depth='.2ex' lspace='-.2em' width='.1em'>
<mrow>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mrow>
</mpadded>
</mrow>
</menclose>
</mtd>
</mtr>
</mtable>
<mspace depth='0.0ex' height='0.0ex' width='2em'/>
<mtable align='top' columnspacing='0em' rowspacing='1ex, -.5ex'>
<mtr>
<mtd></mtd>
<mtd>
<mn>2</mn>
</mtd>
<mtd>
<mn>6</mn>
</mtd>
</mtr>
<mtr>
<mtd>
<mo>−</mo>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mtd>
<mtd>
<mn>5</mn>
</mtd>
<mtd>
<mn>2</mn>
</mtd>
</mtr>
<mtr>
<mtd>
<mrow>
<mo>_</mo>
</mrow>
</mtd>
<mtd>
<mrow>
<mo>_</mo>
</mrow>
</mtd>
<mtd>
<mrow>
<mo>_</mo>
</mrow>
</mtd>
</mtr>
<mtr>
<mtd>
<mphantom>
<mrow>
<mo>+</mo>
<mn>0</mn>
</mrow>
</mphantom>
</mtd>
<mtd>
<menclose class='MathML-Blank' notation='box'>
<mrow>
<mpadded height='-.2ex' depth='.2ex' lspace='-.2em' width='.1em'>
<mrow>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mrow>
</mpadded>
</mrow>
</menclose>
</mtd>
<mtd>
<menclose class='MathML-Blank' notation='box'>
<mrow>
<mpadded height='-.2ex' depth='.2ex' lspace='-.2em' width='.1em'>
<mrow>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mrow>
</mpadded>
</mrow>
</menclose>
</mtd>
</mtr>
</mtable>
</mrow>
</mstyle>
</math>
MathML Markup for Figure 5
<math>
<mrow>
<mstyle mathvariant='sans-serif'>
<mrow>
<mtext>Long Division 3 sumlines, phantoms, cyan fill in digit spaces:</mtext>
</mrow>
</mstyle>
<mspace linebreak='newline' indentalign='left'/>
<mtable align='baseline 2' width='auto' columnalign='right' rowspacing='.25ex' columnspacing='0em'>
<mtr>
<mtd>
<mtext> </mtext>
<mspace mathbackground='#c7eafb' depth='.4ex' height='1.7ex' width='.39em' class='MathML-Blank'/>
<mi> </mi>
<mn>.2</mn>
<mtext> </mtext>
<mspace mathbackground='#c7eafb' depth='.4ex' height='1.7ex' width='.39em' class='MathML-Blank'/>
<mtext> </mtext>
<mphantom>
<mrow>
<mn mathsize='30%'>.</mn>
</mrow>
</mphantom>
</mtd>
</mtr>
<mtr>
<mtd>
<mn>49</mn>
<menclose notation='longdiv'>
<mrow>
<mn>306.25</mn>
</mrow>
</menclose>
</mtd>
</mtr>
<mtr>
<mtd>
<munder>
<mrow>
<mo lspace='0.1em' form='infix'>−</mo>
<mi> </mi>
<mtext> </mtext>
<mspace mathbackground='#c7eafb' depth='.4ex' height='1.7ex' width='.39em' class='MathML-Blank'/>
<mtext> </mtext>
<mi> </mi>
<mn>9</mn>
<mi> </mi>
<mspace mathbackground='#c7eafb' depth='.4ex' height='1.7ex' width='.39em' class='MathML-Blank'/>
<mtext> </mtext>
<mphantom>
<mrow>
<mn>.25</mn>
<mn mathsize='30%'>.</mn>
</mrow>
</mphantom>
</mrow>
<mrow>
<mo>_</mo>
</mrow>
</munder>
</mtd>
</mtr>
<mtr>
<mtd>
<mn>1</mn>
<mphantom>
<mrow>
<mn mathsize='30%'>.</mn>
</mrow>
</mphantom>
<mspace mathbackground='#c7eafb' depth='.4ex' height='1.7ex' width='.39em' class='MathML-Blank'/>
<mphantom>
<mrow>
<mn mathsize='50%'>.</mn>
</mrow>
</mphantom>
<mspace mathbackground='#c7eafb' depth='.4ex' height='1.7ex' width='.39em' class='MathML-Blank'/>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
<mtext>  </mtext>
<mphantom>
<mrow>
<mn>.</mn>
</mrow>
</mphantom>
</mtd>
</mtr>
<mtr>
<mtd>
<munder>
<mrow>
<mo lspace='0.1em' form='infix'>−</mo>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
<mn>98</mn>
<mphantom>
<mrow>
<mn>0.</mn>
</mrow>
</mphantom>
<mtext> </mtext>
</mrow>
<mrow>
<mo>_</mo>
</mrow>
</munder>
</mtd>
</mtr>
<mtr>
<mtd>
<mspace mathbackground='#c7eafb' depth='.4ex' height='1.7ex' width='.39em' class='MathML-Blank'/>
<mtext>  </mtext>
<mtext> </mtext>
<mspace mathbackground='#c7eafb' depth='.4ex' height='1.7ex' width='.39em' class='MathML-Blank'/>
<mtext> </mtext>
<mtext> </mtext>
<mspace mathbackground='#c7eafb' depth='.4ex' height='1.7ex' width='.39em' class='MathML-Blank'/>
<mtext> </mtext>
<mphantom>
<mrow>
<mn mathsize='30%'>...</mn>
</mrow>
</mphantom>
</mtd>
</mtr>
<mtr>
<mtd>
<munder>
<mrow>
<mo lspace='0.1em' form='infix'>−</mo>
<mn>245</mn>
<mphantom>
<mrow>
<mn mathsize='30%'>.</mn>
</mrow>
</mphantom>
</mrow>
<mrow>
<mo>_</mo>
</mrow>
</munder>
</mtd>
</mtr>
<mtr>
<mtd>
<mtext> </mtext>
<mspace mathbackground='#c7eafb' depth='.4ex' height='1.7ex' width='.39em' class='MathML-Blank'/>
<mtext> </mtext>
<mphantom>
<mrow>
<mn mathsize='30%'>.</mn>
</mrow>
</mphantom>
</mtd>
</mtr>
</mtable>
</mrow>
</math>MathML Markup for Figure 6
<math>
<mrow>
<mstyle mathvariant='sans-serif'>
<mrow>
<mtext>Exercise LongDiv Fillin Boxes w/Numbers:</mtext>
<mspace indentalign='left' linebreak='newline'/>
</mrow>
</mstyle>
<mtable columnspacing='.2em' rowspacing='.2ex' columnalign='right' width='auto' align='baseline 2'>
<mtr>
<mtd>
<menclose class='MathML-Blank' notation='box'>
<mrow>
<mpadded height='-.2ex' depth='.2ex' lspace='-.1em' width='.1em'>
<mrow>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mrow>
</mpadded>
</mrow>
</menclose>
<menclose class='MathML-Blank' notation='box'>
<mrow>
<mpadded height='-.2ex' depth='.2ex' lspace='-.1em' width='.1em'>
<mrow>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mrow>
</mpadded>
</mrow>
</menclose>
</mtd>
<mtd>
<mi mathvariant='sans-serif'>R</mi>
<mspace width='.2em'/>
<menclose class='MathML-Blank' notation='box'>
<mrow>
<mpadded height='-.2ex' depth='.2ex' lspace='-.2em' width='.1em'>
<mrow>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mrow>
</mpadded>
</mrow>
</menclose>
</mtd>
</mtr>
<mtr>
<mtd>
<mn>20</mn>
<menclose notation='longdiv'>
<mrow>
<mphantom>
<mrow>
<mi>.</mi>
</mrow>
</mphantom>
<mn>2 8 2</mn>
</mrow>
</menclose>
<mphantom>
<mrow>
<mi mathsize='30%'>.</mi>
</mrow>
</mphantom>
</mtd>
</mtr>
<mtr>
<mtd>
<munder>
<mrow>
<mspace width='-.3em'/>
<mo form='infix'>−</mo>
<mspace width='-.2em'/>
<menclose class='MathML-Blank' notation='box'>
<mrow>
<mpadded height='-.2ex' depth='.2ex' width='.1em'>
<mrow>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mrow>
</mpadded>
</mrow>
</menclose>
<menclose class='MathML-Blank' notation='box'>
<mrow>
<mpadded height='-.2ex' depth='.2ex' lspace='.1em' width='.1em'>
<mrow>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mrow>
</mpadded>
</mrow>
</menclose>
<mphantom>
<mrow>
<mn mathsize='60%'>00</mn>
</mrow>
</mphantom>
</mrow>
<mrow>
<mo>_</mo>
</mrow>
</munder>
</mtd>
</mtr>
<mtr>
<mtd>
<mn>8</mn>
<mphantom>
<mrow>
<mn mathsize='60%'>.</mn>
</mrow>
</mphantom>
<menclose notation='box' class='MathML-Blank'>
<mrow>
<mpadded width='.1em' lspace='-.2em' depth='.2ex' height='-.2ex'>
<mrow>
<mphantom>
<mrow>
<mn>0</mn>
</mrow>
</mphantom>
</mrow>
</mpadded>
</mrow>
</menclose>
<mphantom>
<mrow>
<mn mathsize='30%'>.</mn>
</mrow>
</mphantom>
</mtd>
</mtr>
<mtr>
<mtd>
<munder>
<mrow>
<mo form='infix' lspace='0.1em'>−</mo>
<menclose notation='box' class='MathML-Blank'>
<mrow>
<mpadded width='.1em' lspace='-.2em' depth='.2ex' height='-.2ex'>
<mrow>
<mn>8</mn>
</mrow>
</mpadded>
</mrow>
</menclose>
<menclose notation='box' class='MathML-Blank'>
<mrow>
<mpadded width='.1em' lspace='-.2em' depth='.2ex' height='-.2ex'>
<mrow>
<mn>0</mn>
</mrow>
</mpadded>
</mrow>
</menclose>
</mrow>
<mrow>
<mo>_</mo>
</mrow>
</munder>
</mtd>
</mtr>
<mtr>
<mtd>
<menclose notation='box' class='MathML-Blank'>
<mrow>
<mpadded width='.1em' lspace='-.2em' depth='.2ex' height='-.2ex'>
<mrow>
<mn>2</mn>
</mrow>
</mpadded>
</mrow>
</menclose>
<mphantom>
<mrow>
<mn mathsize='30%'>.</mn>
</mrow>
</mphantom>
</mtd>
</mtr>
</mtable>
</mrow>
</math>
MathML Markup for Figure 8
<math>
<mrow>
<mfrac>
<mrow>
<mrow>
<mo>−</mo>
<mi>b</mi>
</mrow>
<mo>±</mo>
<msqrt>
<mrow>
<msup>
<mrow>
<mi>b</mi>
</mrow>
<mrow>
<mn>2</mn>
</mrow>
</msup>
<mo>−</mo>
<mrow>
<mn>4</mn>
<mo>⁢</mo>
<mi>a</mi>
<mo>⁢</mo>
<mi>c</mi>
</mrow>
</mrow>
</msqrt>
</mrow>
<mrow>
<mn>2</mn>
<mo>⁢</mo>
<mi>a</mi>
</mrow>
</mfrac>
</mrow>
</math>[4] Fans of the TeX programming language like to think that (La)TeX is the solution to all math rendering problems, regardless of publication format. TeX has its problems, however, including the lack of a standardized global implementation on the Web. Rendering engines exist to process some TeX language variants, but few of these engines publish TeX as content directly rendered by web browsers. TeX is not useful in the W3C DOM, limiting overall usefulness in digital content distribution. Further, TeX is not accessible, and also has unique limitations when it comes to rendering elementary math. Further discussion of (La)TeX as a solution to K-12 educational math publishing is beyond the scope of this paper.
[5] http://www.magellanmediapartners.com/venture-capital-private-equity/service-delivery-future-education-publishing/. Oct. 23, 2014.
[6] http://www.knewton.com/press-releases/houghton-mifflin-harcourt-and-knewton-announce-pioneering-partnership/. June 6, 2013.
[7] http://blog.chromium.org/2013/04/blink-rendering-engine-for-chromium.html. Blink: A rendering engine for the Chromium project. April 3, 2013.
[8] https://groups.google.com/forum/#!msg/mozilla.dev.platform/96dZw1jXTvM/hkNn65-Spf4J Enabling support for MathML. September 26, 2012.
[10] http://radar.oreilly.com/2013/11/mathml-forges-on.html. November 1, 2013.
[11] http://docs.mathjax.org/en/latest/misc/epub.html. MathML support on EPUB3 reading systems. 2015.
[12] http://caniuse.com/#feat=mathml. Can I use MathML? May 2015.
[13] http://www.ixl.com/math/grade-2/subtract-two-two-digit-numbers-without-regrouping. Screen capture April 20, 2015.
[14] http://www.d.umn.edu/~lcarlson/atteam/lawsuits.html. Higher Ed Accessibility Lawsuits, Complaints, and Settlements. Laura L. Carlson, 2015.
[15] http://www.accessiq.org/news/news/2015/04/edx-settles-inaccessible-online-courses-case. Access iQ.EdX settles inaccessible online courses case. Tim Lohman, 9 Apr 2015.