Introduction and motivation
Overlapping markup
Overlapping structures are generally recognized as a reality with which structured documents have to deal with. For example, if we want to encode in a single document both the paragraph and page structures of a text, we have to deal with overlapping structures in one way or another. Numerous approaches to tackle the problem have been proposed in the literature or used in practical encoding projects. An excellent survey of such approaches can be found in the introduction of a 2006 EML article by Sperberg-McQueen S2006. Examples include TEI milestones TEI, LMNL (Layered Markup and Annotation Language) of Jennison et al. LMNL, and multi-colored trees of Jagadish et al. J2004.
A number of those solutions involve overlapping markup, i.e., markup in which elements must have matching start- and end-tags, but need not nest properly as in XML. For example, the following document is not well-formed XML, because the elements do not nest properly:
<A>Hello <B>small</A> world!</B>
Yet, it could be considered well-formed in some hypothetical markup language allowing overlap.
Overlap in graphs
Structured documents are often drawn as graphs. Some would say it is one of the best ways to clearly bring out the structure of a document. For authors, it might be one of the most usable representations of a document, in which the nature and meaning of the various manipulations that can be performed on the edited document are most obvious and clear. In fact, most extant structured editors offer a view of the document that can be regarded as a graph representation.
When overlapping markup is allowed in documents, a graph representation becomes even more useful, because arrows can then be used to represent the overlap relationships, which the relative geometric positioning of elements could only awkwardly convey. So, a graph-based user-interface for editing documents with overlapping markup is a sensible idea.
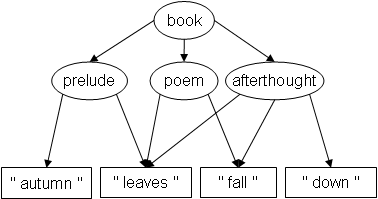
Suppose you have developed a graph-based editor for structured documents with overlapping markup. One day, a minimalist poet composes a document with the following structure:
TexMECS (Huitfeldt and Sperberg-McQueen
HS2003) is a markup language that
allows overlapping elements. It will be discussed in more detail in
the section on TexMECS, but we can say right now that start-tags are of the
form <a| and end-tags of the form |a>. In
TexMECS, the above structure is thus representable as follows:
<book|
<prelude|
autumn
<poem|
<afterthought|
leaves
|prelude>
fall
|poem>
down
|afterthought>
|book>
Leaving out any unmatched tag, the contents of, for example,
afterthought is indeed " leaves fall down ", as the
graph structure says it should; and so on, for all elements.
Feeling particularly Zen that day, the poet decides to thin down
the poem even more by removing " leaves " from the
poem:
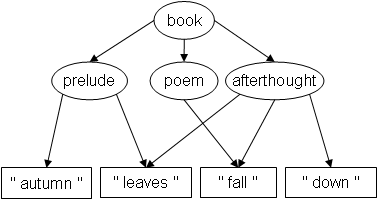
Would your editor allow that arrow removal? Actually, it follows from our Theorem 1 that the resulting structure is not representable at all with overlapping elements in TexMECS.[1]
As the reader may want to verify, any trial-and-error attempt to write a TexMECS document corresponding to the new structure fails, either by aborting, or by producing the following document:
<book|
<prelude|
autumn
<afterthought|
leaves
|prelude>
<poem|
fall
|poem>
down
|afterthought>
|book>
which corresponds to this structure:
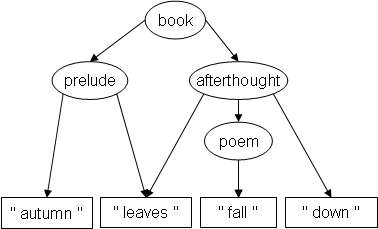
Intuitively, the problem is that we have to start
afterthought before poem starts, and end it after
poem ends, making it impossible not to embed poem
within afterthought. The problem is obvious in this example,
however, the general conditions under which a given graph is serializable with
overlapping elements turn out to be not so simple, as the statement of Theorem
1 shows.
A good editor should at least warn the author when an attempted operation would jeopardize the serializability of the document. For this, a characterization of exactly which graphs are serializable is needed. Without such a characterization, an editor does not know how to determine if the graph is serializable or not.
Overview of this paper
We give here an exact characterization of graphs that are serializable with overlapping markup. As far as we know, it is the first time such a characterization is given. We state a criterion (Theorem 1) which guarantees a graph to be serializable, and which is satisfied by all serializable graphs. By testing this criterion, an editor can verify at all times whether the edited graph is serializable or not.
We also give the inverse characterization (Theorem 2): we show that all well-formed overlapping-markup documents can be obtained by serializing some graph (necessarily satisfying the criterion). Thus, an editor offering only a graph-based interface (and no plain-text view), and allowing only the creation of serializable graphs, would still be complete, in that it would permit the creation of any document representable by overlapping markup.
Our results are formulated in terms of the TexMECS markup language, however, they apply to any markup language (or subset of markup language) allowing overlapping elements.
Related work
Sperberg-McQueen and Huitfeldt SH2004 define a graph model for essentially the same subset of TexMECS as the one we deal with here: the general ordered-descendant directed acyclic graph (GODDAG). They study certain restrictions of the model but do not give an exact characterization of serializable graphs.
Node ordering
It is clear that, in graphs corresponding to documents, at least some ordering of the nodes is important. In the above example, the prelude is "autumn leaves" and not "leaves autumn". In a book, we expect the author to be able to specify the order of the chapters, etc. To account for this, we use node-ordered graphs, in which the children of a node are ordered relative to each other.
One part of our main result (Theorem 1) states it is actually useless, for overlap-only documents, to allow specifying the order of appearance of the nodes over and above that of siblings. In other words, an overlap-only marked-up document is entirely and uniquely determined by the combination of parent-child relationships and sibling ordering. So, for example, an editor for overlap-only documents would offer no extra expressivity by allowing authors to arbitrarily specify the order of appearance of the nodes, over and above specifying the parent-child relationships and ordering siblings.
Basic definitions and notation
Digraphs, DAGs
A directed graph (or digraph) G = (NG, AG) is made up of a set of nodes, NG, and of a set of arcs, AG. The set AG is a subset of (NG × NG) and, thus, determines a binary relation on NG.
Let G = (NG, AG) be a digraph, and b, c, and d, nodes in NG.
Iff (b, c) ∈ AG, we say that c is a child (or direct child) of b, and that b is a parent of c. The fact that c is a child of b is noted b →G c.
Iff both b →G c and b →G d, and c ≠ d, we say that c and d are siblings.
We define the reachability (or dominance) relation of G, noted ⇒G, as the transitive closure of AG. Node c is said to be reachable from, or a descendant of, or dominated by, node b iff b ⇒G c. Node b is said to be an ancestor of node c iff c is a descendant of b.
When G is clear from the context or irrelevant, we may use the notations → and ⇒ instead of, respectively, →G and ⇒G.
Iff b → c, we say that c is directly reachable from b. Iff there exists some d ∈ NG such that b ⇒ d and d ⇒ c, we say that c is indirectly reachable from (or an indirect descendant of) b.
The internal nodes of a digraph are the nodes that have at least one child; its leaves are the nodes without any child; its roots are the nodes that are not a child of any other node.
A cycle-free or acyclic digraph is one in which no node is its own descendant. An acyclic digraph is also called a directed acyclic graph (DAG).
Strict partial orders
Note that, when G is a DAG, ⇒G is a transitive, antireflexive (and hence antisymmetric) binary relation on NG. Such relations are called strict (or antireflexive, or sometimes irreflexive) partial orders on NG. Thus, for all DAG G, ⇒G is a strict partial order on NG.
When R is a strict partial order on NG, we say that b and c are R-ordered (or R-comparable) iff either (b, c) ∈ R or (c, b) ∈ R. Otherwise, we say that they are R-unordered (or R-incomparable). We say R is total (or a strict total order) on NG iff for all b, c ∈ NG, b and c are R-comparable, unless b = c.
For any binary relation R, the fact that (b, c) ∈ R is noted b R c.
Graphs and TexMECS documents
General strategy
To define a correspondence between graphs and TexMECS documents, one option would have been to assign textual labels to the nodes of a graph, and define a serialization algorithm to collect the labels and produce a well-formed TexMECS document. However, we preferred the (essentially equivalent) avenue of requiring an isomorphic mapping between the nodes of a graph and the set of ranges (defined below) that correspond to the various parts of a well-formed TexMECS document. We chose that approach for the following reasons:
-
While a serialization algorithm can be defined in such a way that it always yield a well-formed TexMECS document from a DAG, there exist DAGs for which the element-containment structure of the serialized document does not reproduce the parent-child relationships of the graph. This is in fact a direct corollary of our Theorem 1. Thus, the very notion of correspondence based on a serialization algorithm would be contingent on the structural constraints of Theorem 1.
-
The approach better shields our proofs from the superficial details of the serialization algorithm, and thus, from the “lexical sugar” of the markup language.
Node-ordered DAGs (noDAGs)
We now define a type of graph that allows ordering siblings. Intuitively, this ordering specifies the desired order of appearance of the corresponding elements in the serialized document.
The definition also makes it possible to specify an order among nodes that are not siblings. As noted earlier, one of our results (Theorem 1) entails that, for overlap-only documents, the order among siblings entirely and uniquely determines the order of appearance of all the elements in the document, and that, thus, the extra ordering capability of the graph model does not increase its expressivity. In future work, we plan to investigate other markup formalisms for which the extra ordering capability might increase expressivity.
Definition: Let G be a DAG, and RG a strict partial order on NG. We say that (G, RG) is a node-ordered DAG (noDAG) iff RG is such that, for all b and c ∈ NG, the following holds:
if ((b and c are siblings) or (b and c are distinct roots)), then (b RG c or c RG b)
that is, siblings are totally RG-ordered relative to each other, and so are distinct roots. Some other pairs of nodes may be RG-ordered, but it is not necessary.
Definition: Let (G, RG) be a noDAG. We define the minimal ordering of (G, RG), noted <G, as follows:
<G = {(b, c) ∈ RG | (b and c are siblings) or (b and c are distinct roots)}
Note that <G is a (not necessarily proper) subset of RG. It is also a strict partial order, and it contains exactly those pairs from RG necessary to totally order siblings and distinct roots.
All the examples of noDAGs in this paper have RG = <G. The graphs given as examples earlier in the paper are all noDAGs, with the (minimal) ordering of siblings represented by left-to-right disposition of the arrows going out of the parent node. Unless otherwise stated, the (minimal) ordering of siblings is always represented in that way in our examples.
Notation: In the remainder of this paper, if (G, RG) is a noDAG, the notation G may be used as a shorthand standing for (G, RG), unless it would cause ambiguity.
Definitions: Let G be a noDAG, and b, c, d, and e stand for nodes in NG. Node c is called the first (or leftmost) child of b iff b → c and for no other child d of b is it the case that d <G c. Conversely, c is called the last (or rightmost) child of b iff b → c and for no other node child d of b is it the case that c <G d. We say c and d are consecutive siblings iff there exists b such that b → c, b → d, and for no other node child e of b is it the case that c <G e <G d.
Ranges
A range corresponds intuitively to a stretch of consecutive character positions within some document or character string. Ranges and the associated relations can be defined in various ways; the following definitions suffice for our purposes.
A range is a pair of integers (x, y), where 1 ≤ x ≤ y.
The start-point of a range r = (x, y) is x, and is noted start(r); its end-point is y, and it is noted end(r).
Intuitively, start(r) is the character position in the document where r starts, and end(r) is one more than the position where it ends. So, for all integers x ≥ 1, (x, x) is what we call an empty range.
Range r is said to properly contain range s iff start(r) < start(s) and end(s) < end(r).
Range r is said to precede range s iff start(r) < start(s).
Note that both the proper containment and the precedence relations among ranges are strict partial orders.
Let S be a set of ranges, and r, s ∈ S. We say that r directly contains s with respect to (wrt) S iff the two following statements hold:
1. r properly contains s
2. no t ∈ S is such that r properly contains t and t properly contains s
When the set S is clear from context, we may drop the “with respect to S” part.
We say S has distinct boundaries iff no two distinct ranges in S have the same end-point; that is, iff for all r, s ∈ S, unless (r = s), end(r) ≠ end(s).
Correspondence between a noDAG and a set of ranges
Definition: Let S be a set of ranges. We say that S corresponds to some noDAG G (or, conversely, that G corresponds to S) iff there exists a bijective mapping g between NG and S, such that all of the following conditions hold:
1. (for all b, c ∈ NG) [(b →G c) iff g(b) directly contains g(c) wrt S]
2. (for all b, c ∈ NG) [if (b RG c), then start(g(b)) < start(g(c))]
We then say that G and S correspond to each other through g.
Condition (1) means that the direct containment relationships among the ranges in S correspond exactly to the direct dominance relationships among nodes in G. Condition (2) means that whenever RG specifies an order between two nodes, that order corresponds to the precedence relation on ranges.
Notation: For any b ∈ NG, b' will denote g(b). Conversely, for any r ∈ S, r' will denote g-1(r).
Observation: It is not too difficult to show that if a noDAG and a set of ranges correspond to each other, then they do so through a unique bijection.
TexMECS
Huitfeldt and Sperberg-McQueen introduce TexMECS as “a markup language (or, more precisely, a markup meta-language or family of markup languages) intended for experimental work in dealing with complex documents” HS2003. The main differentiating characteristic of TexMECS, relative to XML, is that it allows elements to overlap, rather than requiring them to nest in a strictly hierarchical way.
We present below a small portion of TexMECS, called overlap-only TexMECS, which includes just enough of the full language to allow overlapping elements. Of interest to readers familiar with the complete language, here are the features of TexMECS excluded from overlap-only TexMECS:
-
virtual elements;
-
interrupted elements;
-
empty elements;
-
attribute specifications;
-
entity references;
-
generic identifier co-indexing (for handling self-overlap);
-
unordered contents;
-
comments.
Please bear in mind that TexMECS is an experimental language, and may evolve in the future.
All our results are stated—and proved—relative to overlap-only TexMECS, but clearly, they would hold mutatis mutandis for any equivalent formalism. At least at first glance, there is no reason to believe that throwing in all but the two first features from the above list would cause any major problem (aside from adding nitty-gritty details to the proofs). Our proofs do not apply—and, in fact, we strongly suspect the results do not hold (although we propose no formal proof of this)—if we add interrupted elements and/or virtual elements.
Overlap-only TexMECS
The following are adapted or taken from Huitfeldt and Sperberg-McQueen HS2003.
Start-tags are of the form <a| and end-tags of
the form |a>, where a stands for any acceptable
XML generic identifier. Two tags (start- or end-) are said to
match iff they bear the same generic
identifier.
The depth of any tag T in a document is defined as the difference:
(number of start-tags matching T and occurring at or before T in the document)
− (number of end-tags matching T and occurring before T in the document)
A character string is said to be a well-formed overlap-only TexMECS document iff all of the following conditions hold:
-
There are equal numbers of start- and end-tags.
-
No tag has depth 0.
-
The document starts with a tag and ends with a tag.
Note that, under those definitions, the following are well-formed:
-
<A|a<B|b|A>c|B> -
<A|a|A>abc<B|b|B> -
<A||A><B||B>
but not the following:
-
abc -
a<A||A> -
<A||A>a
A start-tag S and another tag E are said to correspond (or be paired) to each other iff E is the tag closest to S among those that both (1) occur after S in the document; (2) match S; and (3) have the same depth as S. It can be shown that, in well-formed documents, every tag corresponds to exactly one other tag, and that corresponding tags have opposite polarities (one is a start-tag and the other is an end-tag).
Correspondence between a noDAG and a TexMECS document
Definition: Let D be a well-formed overlap-only TexMECS document. We define the set of ranges associated to D, noted ranges(D), as the set containing exactly the following ranges:
1. For each start-tag in D, a range going from the first character of the start-tag up to (and including) the last character of the matching end-tag.
2. For each start-tag in D not followed immediately by another start-tag, a range going from the character immediately following the start-tag up to (and excluding) the first character of the next upcoming tag (start- or end-).
3. For each end-tag in D not followed immediately by another tag, a range going from the character immediately following the end-tag up to (and excluding) the first character of the next upcoming tag (start- or end-).
Note that (2) will introduce an empty range for each start-tag immediately followed by an end-tag, and that no other configuration of tags will introduce an empty range.
Definition: We say that a well-formed overlap-only TexMECS document D corresponds to some noDAG G (or, conversely, that G corresponds to D) through some mapping g iff ranges(D) corresponds to G through g.
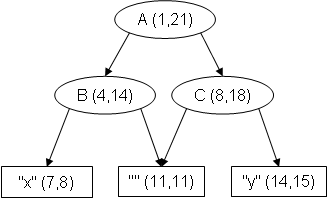
Example: Let D be the following well-formed TexMECS document (character positions given underneath, for ease of reference):
<A|<B|x<C||B>y|C>|A> 000000000111111111122 123456789012345678901
Then, ranges(D) will contain six ranges:
-
(1,21) corresponding to element
A; -
(4,14) corresponding to element
B; -
(8,18) corresponding to element
C; -
(7,8) corresponding to character
x; -
(11,11) corresponding to the empty string between
<C|and|B>; -
(14,15) corresponding to character
y.
The reader can readily verify that the set ranges(D) corresponds to the following noDAG (through the bijection implicitly defined above):
Observation 1: For all well-formed overlap-only TexMECS document D, the set ranges(D) has distinct boundaries. This follows simply from our definition of ranges(D) and the fact that TexMECS end-tags have positive length. Note that no two ranges in ranges(D) have the same start-point either, but, because of the way our various definitions are set up, we do not need this in our proofs.
Empty strings and spurious overlap
Intuitively, the ranges we associate with a document are the various “locations” in the document where its contents are situated. We have chosen to consider that the empty string is “content” only when located between a start-tag and an adjacent following end-tag. This seems to us the most natural point of view.
However, one can view things differently; for example, it could be considered that the empty string between any two adjacent tags is content. Looking at things this way, the document in the above example would have two more ranges: (4,4) and (18,18), and accordingly, the corresponding noDAG would have two more nodes.
Why would one want to do that? One answer is that it allows
discussing spurious overlap in terms of
graphs. Sperberg-McQueen and Huitfeldt
SH2004 define spurious overlap as
the use of overlapping elements in places where properly-nesting elements would
have adequately represented an “equivalent” structure. For
example, the above document contains spurious overlap, because flipping the
<C| and |B> tags would eliminate the overlap,
yet only change the hierarchical positioning of an empty string. Another tag
configuration considered spurious overlap is illustrated in the following
document:
<A|<B|xyz|A>|B>
Here, flipping either the start- or end-tags would result in
properly-nesting elements, while preserving the fact that all three data
characters are within both an A element and a B
element.
In order to define precisely spurious overlap in terms of graphs, Sperberg-McQueen and Huitfeldt naturally take the approach that there is empty content between any two adjacent tags, then define appropriate conditions on graphs that correspond to spurious overlap.
We are convinced that, in general, spurious overlap can have distinctive meaningful semantics, and thus, should not be forbidden. Nevertheless, we recognize it can be useful to detect it, for example, as a helper function for authors, or when it is known to be unintentional SH2004. With our current definition of ranges(D) and the ensuing graph representation of a document, the discussion of spurious overlap found in SH2004 cannot be held directly. To change this, we would simply need to define ranges(D) so that an empty range is introduced for any two adjacent tags. Our results would still hold, except that the statement of Theorem 1 would need to include the additional condition that the first and last child of any internal node are both leaves (they could be the same leaf).[2]
Results
Completion-acyclic noDAGs
We now introduce a class of noDAGs that is central in our characterization.
Let G be a noDAG, and b, c, and d, nodes in NG.
We define two relations, derived from G, which we call collectively the completions of G. One is the starts-before- (or SB-) completion of G, and is noted SB(G); the other is the ends-after- (or EA-) completion of G, and is noted EA(G). The rationale for those names will become clear later.
Definition: Relation SB(G) is the transitive closure of the union of the following sets:
1. AG
2. <G
3. {(b, c) | (∃d)[(d ⇒ b) & (d <G c)] & c ⇏ b}
Notation: For convenience, the third set above will be noted CSB(G).
Definition: Relation EA(G) is the transitive closure of the union of the following sets, where >G denotes the inverse relation of <G:
1. AG
2. >G
3. {(b, c) | (∃d)[(d ⇒ b) & (d >G c)] & c ⇏ b}
Notation: For convenience, the third set above will be noted CEA(G).
Note that the only difference between the two preceding definitions is that, for EA(G), >G is used instead of <G.
As will be shown in the examples below, the completions of a noDAG are not necessarily cycle-free, when seen as arcs linking the nodes of G. The case where they are is, however, of particular interest, so we define the following.
Definition: A noDAG G is said to be completion-acyclic iff both digraphs (NG, SB(G)) and (NG, EA(G)) are acyclic.
Examples
In the upcoming examples (as in the earlier ones), the ordering of siblings is represented by left-to-right disposition of the arrows going out of the parent node. In the completions, this ordering (or its inverse) appears explicitly as added arcs.
The arcs added to form the completions are shown in red, but most added arcs obtainable by transitivity are not shown, to increase readability. For each example, we first show the original graph, then the starts-before completion, then the ends-after completion.
The first two examples use the same graph structures as earlier examples.
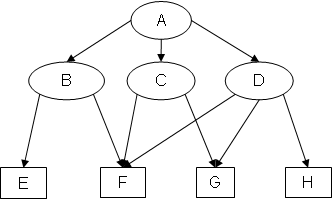
Example 1: Original graph EX1
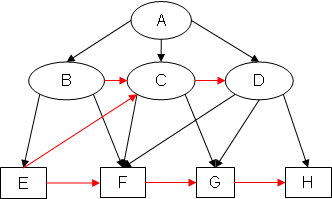
Example 1: SB(EX1)
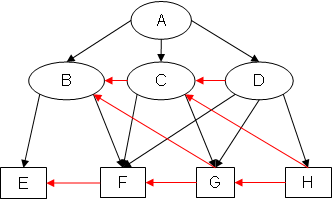
Example 1: EA(EX1)
Notice how, for example, in SB(EX1), arc EC has been added because (B <G C) & (B ⇒ E) & (C ⇏ E), and in EA(EX1), arc GB has been added because (C >G B) & (C ⇒ G) & (B ⇏ G).
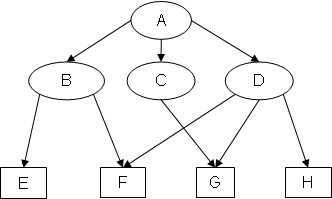
Example 2: Original graph EX2
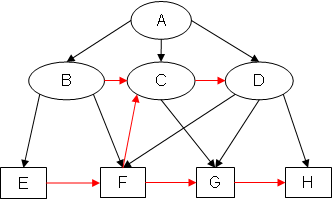
Example 2: SB(EX2)
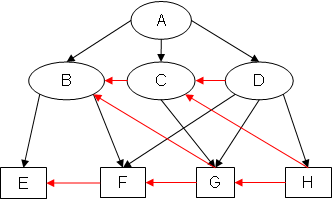
Example 2: EA(EX2)
Notice how, in SB(EX2), the added arcs CD and FC form the cycle CDFC.
The third example shows a noDAG for which the SB-completion has no cycle, but the EA-completion has one.
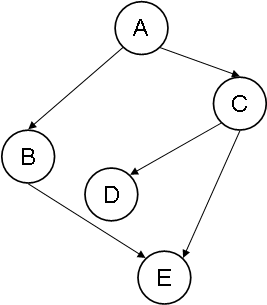
Example 3: Original graph EX3
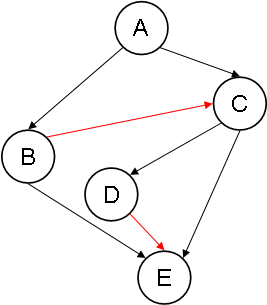
Example 3: SB(EX3)
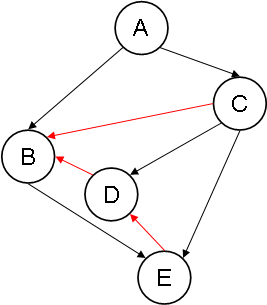
Example 3: EA(EX3)
Notice how, in EA(EX3), the added arcs ED and DB form the cycle BEDB.
Since both completions of EX1 are cycle-free, EX1 is completion-acyclic. Because at least one completion of EX2 and EX3 has a cycle, neither EX2 nor EX3 is completion-acyclic.
Main results
Before we get to our main results, we need to establish preliminary results.
Lemma 1: Let G be a noDAG to which some set of ranges corresponds. Then, no node in G is both directly and indirectly dominated by some other node.
Proof. Immediate by the definitions of correspondence and of direct containment.
QED (Lemma 1)
Corollary 1 to Lemma 1: Let G be a noDAG to which some set of ranges S corresponds. Then, for all b, c ∈ NG, if (b <G c), then b ⇏G c.
Proof. By the definition of <G, if (b <G c), then either b and c are both roots, or they are siblings. If c is a root, then, clearly b ⇏G c. If b and c are siblings, then (b ⇒G c) would contradict the lemma.
QED (Corollary 1 to Lemma 1)
Corollary 2 to Lemma 1: Let G be a noDAG to which corresponds some set of ranges with distinct boundaries S through g. Then, for all b, c ∈ NG, if (b <G c), then end(b') < end(c').
Proof. By Corollary 1, b ⇏G c. By the definitions of a noDAG and of correspondence, we know that start(b') < start(c'). But end(c') < end(b') would imply b ⇒G c. So, we must conclude that end(b') ≤ end(c'). Since S has distinct boundaries, we conclude that end(b') < end(c').
QED (Corollary 2 to Lemma 1)
Lemma 2: Let G be a noDAG to which corresponds some set of ranges with distinct boundaries S through g. Then, for all r, s ∈ NG, the following two conditions hold:
1- if (r, s) ∈ SB(G), then start(r') < start(s')
2- if (r, s) ∈ EA(G), then end(r') > end(s')
Proof. We will prove the lemma only for SB(G); the proof for EA(G) is entirely similar (but makes use of Corollary 2 to Lemma 1).
By the definition of starts-before-completion, we know that:
SB(G) = transitive-closure(AG ∪ <G ∪ CSB(G)).
We will prove that (1) above holds for each arc in (AG ∪ <G ∪ CSB(G)). Then, by transitivity of < on integers, the lemma will follow.
For all arcs (r, s) ∈ (AG ∪ <G), then clearly, by the appropriate definitions, start(r') < start(s'). There remains to treat the case where (r, s) ∈ CSB(G). We prove this by contradiction.
Suppose that (r, s) ∈ CSB(G) and start(s') ≤ start(r'). By the definition of CSB(G), there must exist d such that (d ⇒ r) & (d <G s) & s ⇏ r.
From (d <G s), by Corollary 1 to Lemma 1, we conclude that d ⇏ s.
Since, by hypothesis, s start(s') ≤ start(r'), and because s ⇏ r, we conclude that end(s') ≤ end(r'). Because d ⇒ r, we know that end(r') ≤ end(d'). Thus, end(s') ≤ end(d'). But d <G s implies that start(d') < start(s'). Thus, we conclude that d ⇒ s, a contradiction.
We must thus reject the hypothesis that start(s') ≤ start(r'), and conclude that, for all arcs (r, s) ∈ CSB(G), start(r') < start(s').
QED (Lemma 2)
Lemma 3: Let G be a finite noDAG. Then, for all distinct b, c ∈ NG, both of the following hold:
a) At least one of the pairs (b, c) and (c, b) is in SB(G).
b) At least one of the pairs (b, c) and (c, b) is in EA(G).
Proof. Here again, we will prove the lemma only for SB(G), the proof for EA(G) being entirely similar.
Let G be a noDAG, and S = SB(G). The proof is simpler if G has only one root, and it generalizes easily (though somewhat tediously) to the cases where G has more than one root. So, we will treat only the case where G has a unique root.
Let distinct b, c ∈ NG. If either b ⇒G c or c ⇒G b, then, by definition, one of (b, c) and (c, b) ∈ S. There remains to treat the case where b and c are (⇒G)-incomparable. Suppose they are, and let m be a (⇒G)-minimal-upper-bound (mub) of b and c.[3]
Suppose, without loss of generality, that neither b nor c is a child of m (if either is, similar—and actually simpler—arguments lead to the same conclusions). Then, by the definition of mub, and because b and c are (⇒G)-incomparable, there must exist e, f ∈ NG such that (m → e ⇒ b) & (m → f ⇒ c) & (f ⇏ b) & (e ⇏ c). Since e and f are siblings, they are <G-comparable. If, on the one hand, e <G f, then, we have:
(e ⇒ b) & (e <G f) & (f ⇏ b)
and, thus, by construction of S, (b, f) ∈ S, and, by transitivity, (b, c) ∈ S. If, on the other hand, f <G e, then, we have:
(f ⇒ c) & (f <G e) & (e ⇏ c)
and, thus, by construction of S, (c, e) ∈ S, and, by transitivity, (c, b) ∈ S.
QED (Lemma 3)
Corollary to Lemma 3: Both completions of a finite completion-acyclic noDAG G are strict total orders on NG.
Proof. By the definition, both completions of a completion-acyclic noDAG are cycle-free. Thus, it is immediate that they are antireflexive and antisymmetric. Since they are obtained by transitive closure, they are transitive. It follows from the lemma that they are total.
QED (Corollary to Lemma 3)
Lemma 4: For all completion-acyclic noDAG G, SB(G) ∩ EA(G) = (⇒G).
Proof. Let G be a completion-acyclic noDAG. By the definitions of the respective completions, it suffices to show that no pair (b, c) can be both in CSB(G) and CEA(G).
We prove this by contradiction: suppose there exists a pair (b, c) that is a member of both sets. Since (b, c) is in CSB(G), then it is also in SB(G), by definition. Because it is in CEA(G), we know that c ⇏ b, and that there exists d such that c <G d and d ⇒G b. From this and the definition of SB(G), we conclude that the pair (c, b) is in SB(G). So, both (b, c) and (c, b) are in SB(G). Hence, SB(G) contains a cycle, which contradicts the hypothesis that G is completion-acyclic.
QED (Lemma 4)
Lemma 5: Let G be a finite completion-acyclic noDAG. For all (b, c) ∈ NG, if (b, c) ∈ SB(G) but b ⇏ c, then any node dominated by b and not by c precedes, in SB(G)-order, c and any node dominated by c. Conversely, if (b, c) ∈ EA(G) but b ⇏ c, then any node dominated by b and not by c precedes, in EA(G)-order, c and any node dominated by c.
Proof. Let G be a finite completion-acyclic noDAG. First observe that, by Corollary to Lemma 3 and Lemma 4, for all distinct, ⇒-incomparable b, c ∈ NG, if (b, c) ∈ SB(G), then (c, b) ∈ EA(G), and vice-versa.
Again, we prove the lemma only for SB, the proof for EA being entirely similar. Let b and c be as in the statement of the lemma, and suppose d and e are such that b ⇒ d, c ⇏ d, c ⇒ e. Note that d ⇏ c. Suppose, for the sake of contradiction, that (c, d) ∈ SB(G). Then, by the preceding observation, we have (d, c) ∈ EA(G), (c, b) ∈ EA(G), and, because b ⇒ d, (b, d) ∈ EA(G). Thus, there is a cycle in EA(G), contradicting the fact that G is completion-acyclic. So, by Corollary to Lemma 3, we must conclude that (d, c) ∈ SB(G), and thus, by transitivity, that (d, e) ∈ SB(G).
QED (Lemma 5)
Theorem 1: Let (G, RG) be a noDAG. Then, there exists a well-formed overlap-only TexMECS document corresponding to G iff all of the following hold:
1- NG is finite and non-empty.
2- No node of G is both directly and indirectly reachable from some other node.
3- G is completion-acyclic.
4- RG is a subset of SB(G).
5- No two leaves are consecutive in both SB(G)-order and reverse EA(G)-order.
6- Neither the first nor the last root of G (in <G order) is a leaf.
Note that point (4) asserts that the ordering among nodes specified by RG − (<G) can only confirm what is already implicit in <G. Points (5) and (6) may seem mysterious at first, but simply translate idiosyncratic morphological contingencies of well-formed overlap-only TexMECS. An alternate formulation of point (5) is that no two consecutive siblings are leaves with the same set of parents.
Proof.
(⇒) Let (G, RG) be a noDAG to which corresponds a well-formed overlap-only TexMECS document D. We show in succession that G satisfies conditions (1) to (6) in the statement of the theorem.
(1): Follows immediately from the various definitions.
(2): Follows immediately from Lemma 1.
(3): Follows from Lemma 2 (which, by Observation 1, we know is applicable) because, if either SB(G) or EA(G) had a cycle, it would imply that, for some r ∈ ranges(D), start(r) < start(r) or end(r) < end(r).
(4): By (1) and (3), G is finite and completion-acyclic. Thus, Corollary to Lemma 3 applies, and we conclude that SB(G) is a strict total order on NG. Since SB(G) is total, any pair (r, s) that is not in it can only contradict it. Suppose, then, there exists a pair (r, s) ∈ RG − SB(G). By the preceding argument, we conclude that (s, r) ∈ SB(G). So, by Lemma 2, start(s') < start(r'). However, by the definition of correspondence, (r, s) ∈ RG implies that start(r') < start(s'), a contradiction.
(5): Proof sketch. Suppose, for the sake of contradiction, that there exist two leaves v and w in G consecutive in both SB(G)-order and reverse EA(G)-order. Suppose, without loss of generality, that v and w are not roots. Then, it is not hard to see that v' and w' must be both directly contained (wrt ranges(D)) in some other range, without any range starting and/or ending between them. But, by construction of ranges(D), this is impossible.
(6): We treat only the case of the first root; the proof for the last root is entirely similar. It is easy to show that, in a completion-acyclic noDAG, the first node in SB-order is always the first root. So, if r is the first root of G, in <G order, then r is the first node in SB(G)-order. By Lemma 2 and the construction of ranges(D), then, start(r') = 1. Because D is well-formed, it must start with a tag; thus, r is not a leaf.
(⇐) Proof sketch. Let (G, RG) be a noDAG satisfying conditions (1) to (6) in the statement of the theorem. We construct a well-formed overlap-only TexMECS document D and show it corresponds to G.
We sketch informally the construction of D.
We start by assigning an arbitrary, distinct, generic identifier to each internal node of G. Then, on each side (left and right) of the node, we stick TexMECS tags derived from the generic identifier: a start-tag on the left, and an end-tag on the right; for example “<QC|” on the left and “|QC>” on the right.
Then, we let those tags slide down from their node, following the arrow linking the node to its first child (for a start-tag) and to its last child (for an end-tag). When a tag arrives to a new internal node, it continues sliding down, using the same arrow position (first or last) as initially, all the way down, until it ends up on a leaf. When it does, it goes to the left of the leaf (if it is a start-tag), or to its right (if it is an end-tag), and stays there.
After both tags of all internal nodes have slid down to a leaf, we order the start-tags on the left of each leaf in SB(G) order of the node they come from. Then, we order the end-tags on the right of each leaf in reversed EA(G) order of the node they come from.
Then, for each leaf, we create a character string consisting of the concatenation of all the start-tags to its left, in order, then, the character “A”, then all the end-tags to its right, again in order.
Finally, we pick-up and concatenate the strings created for the leaves, in SB(G) order. That is our document D.
The mapping g between ranges(D) and NG is the one that maps to each internal node the range stretching from one to the other of (and including) the two tags that originate from it, and to each leaf the character “A” that it contributed to D.
To see that D is a well-formed overlap-only TexMECS document, observe that: (1) there are equal numbers of start- and end-tags; (2) all generic identifiers are distinct, and thus, the fact (following from Lemma 5) that any start-tag occurs to the left of the matching end-tag suffices to guarantee that no tag has depth 0; and (3) the document starts and ends with a tag.
We now sketch a proof that the set ranges(D) corresponds to G through g, i.e., that the following statements both hold:
i. (for all b, c ∈ NG) [(b →G c) iff (b' directly contains c') wrt ranges(D)]
ii. (for all b, c ∈ NG) [if (b RG c), then start(b') < start(c')]
To prove (i), we will show that proper containment on ranges(D) corresponds to reachability on G. Since, by hypothesis, G contains only direct reachability relationships, (i) will follow.
Suppose first that b ⇒G c. Then, by construction of D, Lemma 5, and the fact that b precedes c in SB(G)-order, start(b') < start(c'). Likewise, end(c') < end(b'). Thus, b' properly contains c'.
Now suppose for some r and s in ranges(D), r properly contains s. By construction of D, and Lemma 5, it can be show that r' ⇒G s'.
To prove (ii), we will show that for all (b, c) ∈ SB(G), start(b') < start(c'). Since, by hypothesis, RG is a subset of SB(G), (ii) will follow. By transitivity of < on integers, it suffices to show that for all (b, c) ∈ (AG ∪ <G ∪ CSB(G)), start(b') < start(c'). For each of the three sets constituent of the union, the desired result follows from Lemma 5.
QED (Theorem 1)
Theorem 2: Every well-formed overlap-only TexMECS document corresponds to some noDAG satisfying all the conditions in the statement of Theorem 1.
Proof sketch. From D, any well-formed overlap-only TexMECS document, first compute ranges(D), then the direct containment relationships between the members of ranges(D). Construct a noDAG (G, RG) as follows:
1. NG = ranges(D)
2. For all r, s ∈ N, r → s iff r directly contains s
3. For all r, s ∈ N, r RG s iff start(r) < start(s)
It is easily seen that (G, RG) corresponds to D through the identity function. Note that (G, RG) necessarily satisfies all the conditions in the statement of Theorem 1, since it corresponds to a well-formed, overlap-only TexMECS document.
QED (Theorem 2)
Serializability and leaves
Defining restrictions on DAGs by requiring the existence of some special ordering of the leaves, or by restricting which nodes dominate which leaves, or both, is quite natural. For example, with a slightly different data structure than noDAGs (GODDAGs), Sperberg-McQueen and Huitfeldt SH2004 define interesting restrictions through criteria involving the sets of leaves dominated by internal nodes.
The following example, however, shows that no criteria involving only the leaves can guarantee serializability for noDAGs in general. We exhibit (Figure 9) a noDAG with only one leaf, which is not completion-acyclic and, thus, by Theorem 1, not serializable. As can be seen on Figure 10, its SB-completion has the cycle CDFC (here again, added arcs obtainable by transitivity are not shown).
Figure 9. Non-completion-acyclic noDAG with only one leaf.
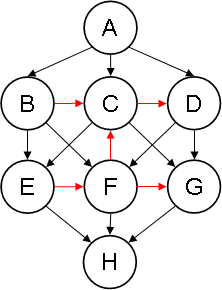
Figure 10. SB-completion of the noDAG on Figure 9.
Applications
Perhaps the most important application of this characterization is to allow the precise definition of a DOM (document object model) for overlapping markup documents, and the inclusion of serializability verification functions in software products (editors, etc.) based on a DOM representation of documents.
Among other things, it would allow a graph-interface document editor to determine whether or not some node-oriented operation attempted by an author (node creation or displacement) preserves the serializability of the graph.
Another application area is the validation of documents. Validation is usually defined on the serialized form of documents. However, in some cases, validation on the graph (or DOM) structure is preferable. To be able to define validation mechanisms on the graphs of documents, it is important to know precisely the structural properties of exactly those graphs that the validation mechanism must be able to handle. The kind of characterization we provide here is a useful and precise description of the exact class of graphs that all validation mechanisms must be able to deal with.
Conclusion and future work
In this article, we established a necessary and sufficient condition for a node-ordered graph (noDAG) to correspond to the structure of an overlapping markup document, such as a well-formed TexMECS document that uses only overlapping markup (and no interrupted or virtual elements). That characterization provides a criterion which graph-based (e.g., DOM-based) applications can test to determine if a graph can be serialized into a document using only overlapping markup. Future work includes establishing the complexity of testing the criterion and finding optimal algorithms to do so.
A consequence of that characterization is that, for overlap-only markup, no expressivity is to be gained by allowing authors to arbitrarily order the nodes, over and above specifying the parent-child relationships and ordering siblings, as those two combined determine entirely and uniquely the serialized document.
We also showed that all well-formed overlapping-markup documents can be obtained by serializing some graph that satisfies the criterion. Thus, an editor offering only a graph-based interface (and no plain-text view), and allowing only the creation of graphs that satisfy the criterion, would still be complete, in that it would permit the creation of any well-formed overlapping-markup document.
A corollary to our proofs is that round-tripping between noDAGs and TexMECS documents is possible. This means that algorithms can be given to transform any TexMECS document into a (labelled) noDAG, and any serializable (labelled) noDAG into a TexMECS document, in such a way that applying the two transformations one after the other will give essentially the original object. Developing efficient algorithms to do this, and appropriate definitions of canonical forms is something we want to investigate in the future.
We also believe that relaxing somewhat the conditions in Theorem 1 could characterize variants of overlap-only TexMECS, for example, a variant in which overlapping markup is prohibited, but interrupted elements are allowed. This is also on the future work agenda.
Finally (and this is actually what brought us to overlapping markup in the first place), we would like to investigate what sort of “natural” intertextual semantics might be defined for overlapping markup.
Acknowledgements
The author thanks Claus Huitfeldt and Lars Johnsen for exciting and fruitful discussions, as well as useful comments on drafts of this paper.
References
[HS2003] Claus Huitfeldt and C. M. Sperberg-McQueen. “TexMECS: An experimental markup meta-language for complex documents.” (2003) http://decentius.aksis.uib.no/mlcd/2003/Papers/texmecs.html
[J2004] Jagadish, H. V., Laks V. S. Lakshmanan, Monica Scannapieco, Divesh Srivastava, and Nuwee Wiwatwattana. “Colorful XML: One hierarchy isn't enough.” Proceedings of the 2004 ACM SIGMOD International conference on management of data. (2004) http://doi.acm.org/10.1145/1007568.1007598
[S2006] C. M. Sperberg-McQueen. “Rabbit/duck grammars: a validation method for overlapping structures.” Proceedings of the 2006 Extreme Markup Languages conference. (2006) http://www.idealliance.org/papers/extreme/proceedings/html/2006/SperbergMcQueen01/EML2006SperbergMcQueen01.html
[SH2004] C. M. Sperberg-McQueen and Claus Huitfeldt. “GODDAG: A Data Structure for Overlapping Hierarchies.” In: P. King and E.V. Munson (Eds.): DDEP-PODDP 2000, Lecture Notes in Computer Science 2023, Springer-Verlag, pp. 139-160. (2004)
[TEI] Text Encoding Initiative Consortium. TEI Guidelines for Electronic Text Encoding and Interchange. http://www.tei-c.org/Guidelines/
[LMNL] Jeni Tennison, Gavin Thomas Nicol, and Wendell Piez. LMNL (Layered Markup and Annotation Language) Tutorial. http://lmnl.net/prose/tutorial/
[1] It is representable in TexMECS, but only with features more powerful than overlapping markup; see the section on TexMECS.
[2] The proofs, however, would need to be slightly more complex, because the set ranges(D) would not necessarily have distinct boundaries any more.
[3] A (⇒G)-minimal-upper-bound (mub) of b and c is any node m such that (m ⇒G b) and (m ⇒G c), and such that, for all descendants e of m, (e ⇏ b) or (e ⇏ c). Since we assumed G is finite and has a single root, a simple argument shows that at least one (⇒G)-mub exists for all b and c.